
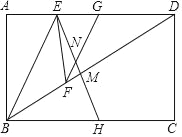
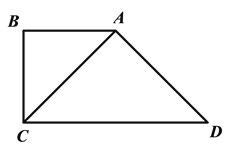
【题目】如图,在矩形ABCD中,EH垂直平分BD,交BD于点M,过BD上一点F作FG∥BE,FG恰好平分∠EFD,FG与EH交于点N.
(1)求证:DEDG=DFBF;
(2)若AB=3,AD=9,求FN的长.
【答案】(1)证明见解析;(2)FN=![]() .
.
【解析】分析:(1)由线段垂直平分线的性质可得BE=DE,根据等边对等角得出∠1=∠2.再证明∠3=∠5,那么△BEF∽△DFG,根据相似三角形对应边成比例可得![]() =
=![]() ,将BE=DE代入即可证明DEDG=DFBF;
,将BE=DE代入即可证明DEDG=DFBF;
(2)设DE=x,则BE=x,在Rt△ABE中根据勾股定理得出32+(9-x)2=x2,解方程求出x=5.在Rt△ABD中,由勾股定理求出BD=![]() =
=![]() ,那么BM=DM=
,那么BM=DM=![]() .再证明BE2=BFDB,求出BF=
.再证明BE2=BFDB,求出BF=![]() =
=![]() ,那么FM=BM-BF=
,那么FM=BM-BF=![]() .再由FN∥BE,得出△MNF∽△MEB,根据相似三角形对应边成比例可得
.再由FN∥BE,得出△MNF∽△MEB,根据相似三角形对应边成比例可得![]() =
=![]() ,即可求出FN=
,即可求出FN=![]() .
.
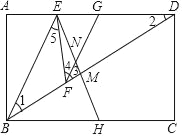
详解:(1)证明:如图.∵EH垂直平分BD,
∴BE=DE,∠1=∠2.
∵FG平分∠EFD,
∴∠3=∠4.
∴FG∥BE,
∴∠4=∠5,
∴∠3=∠5,
∴△BEF∽△DFG,
∴![]() =
=![]() ,
,
∵BE=DE,
∴![]() =
=![]() ,
,
∴DEDG=DFBF;
(2)解:设DE=x,则BE=x,
∵AB=3,AD=9,
∴AE=9﹣x.
在Rt△ABE中,∵∠A=90°,
∴AB2+AE2=BE2,即32+(9﹣x)2=x2,
解得x=
在Rt△ABD中,∵∠A=90°,AB=3,AD=9,
∴BD=![]() =3
=3![]() ,
,
∴BM=DM=![]() .
.
由(1)得![]() =
=![]() ,
,
∵FG∥BE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵BE=DE,
∴BE2=BFDB,
∴BF=![]() =
=![]() =
=![]() ,
,
∴FM=BM﹣BF=![]() ﹣
﹣![]() =
=![]() .
.
∵FN∥BE,
∴△MNF∽△MEB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得FN=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
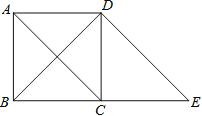
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
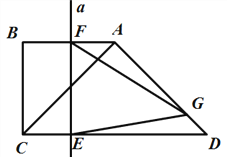
【题目】两个等腰直角三角形如图放置,∠B=∠CAD=90°,AB=BC=![]() cm,AC=AD,垂直于CD的直线a从点C出发,以每秒
cm,AC=AD,垂直于CD的直线a从点C出发,以每秒![]() cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).
cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).
(1)填空:CD=_______cm;
(2)连接EG、FG,设△EFG的面积为y,求y与t之间的函数关系式,并写出相应t的取值范围;
(3)是否存在某一时刻t(0<t<2),作∠ADC的平分线DM交EF于点M,是否存在点M是EF的中点?若存在,求此时的t值;若不存在,请说明理由。
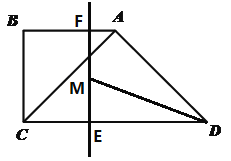
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是一个直角,作射线
是一个直角,作射线![]() ,再分别作
,再分别作![]() 和
和![]() 的平分线
的平分线![]() ,
,![]() .
.
(1)如图①,当![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当射线![]() 在
在![]() 内绕
内绕![]() 点旋转时,
点旋转时,![]() 始终是
始终是![]() 与
与![]() 的平分线.则
的平分线.则![]() 的大小是否发生变化,说明理由;
的大小是否发生变化,说明理由;
(3)当射线![]() 在
在![]() 外绕
外绕![]() 点旋转且
点旋转且![]() 为钝角时,
为钝角时,![]() 仍始终是
仍始终是![]() 与
与![]() 的平分线,直接写出
的平分线,直接写出![]() 的度数(不必写过程).
的度数(不必写过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+2 与x轴交于A,B两点,与y轴交于点C,AB=4.矩形OADC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的表达式;
(2)点P是直线EO 上方抛物线上的一个动点,作PH⊥EO,垂足为H,求PH的最大值;
(3)点M在抛物线上,点N在抛物线的对称轴上,若四边形ACMN是平行四边形,求点M、N的坐标.
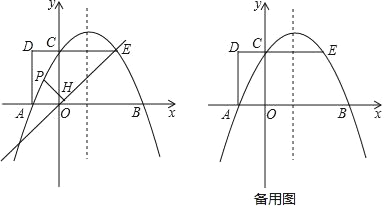
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要印制商品宣传材料,甲印刷厂的收费标准是:每份材料收1元印制费,另收1 500元制版费;乙印刷厂的收费标准是:每份材料收2.5元印制费,不收制版费.
(1)分别写出两厂的收费y(元)与印制数量x(份)之间的关系式;
(2)在同一直角坐标系中画出它们的图象;
(3)根据图象回答下列问题:印制800份宣传材料时,选择哪一家印刷厂比较合算?商场计划花费3 000元用于印刷上述宣传材料,找哪一家印刷厂印制宣传材料多一些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )

A. 3 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市政府对城市建设进行了整改,如图,已知斜坡AB长![]() 米,坡角(即∠ABC)为45°,AC⊥BC,现计划在斜坡中点M处挖去部分斜坡,修建一个平行于水平线CB的休闲平台MN和一条新的斜坡AN.(温馨提示:后两个小题结果都保留根号)
米,坡角(即∠ABC)为45°,AC⊥BC,现计划在斜坡中点M处挖去部分斜坡,修建一个平行于水平线CB的休闲平台MN和一条新的斜坡AN.(温馨提示:后两个小题结果都保留根号)
(1)若修建的斜坡AN的坡比为![]() ,求休闲平台MN的长是多少米?
,求休闲平台MN的长是多少米?
(2)一座建筑物GH距离B点34米远(BG=34米),小亮在M点测得建筑物顶部H的仰角(即∠HME)为30°.点A、C、B、G,H在同一个平面内,点C、B、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
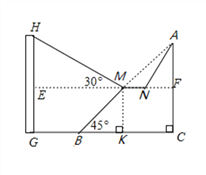
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com