
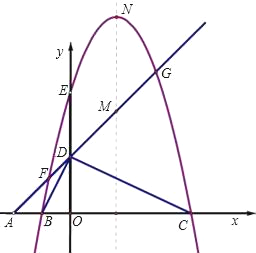
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
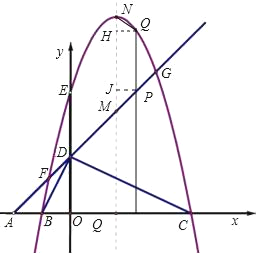
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
【答案】(1)y=﹣x2+3x+4;(2)点P坐标是(﹣1+![]() ,1+
,1+![]() )或(2,4);(3)①菱形不存在,理由见解析;②能成为等腰梯形,点P的坐标是(2.5,4.5).
)或(2,4);(3)①菱形不存在,理由见解析;②能成为等腰梯形,点P的坐标是(2.5,4.5).
【解析】分析:(1)利用待定系数法列方程组求二次函数的解析式.(2)利用勾股定理的逆定理,判断直角三角形.(3)分别设出P,Q点坐标,按照菱形的条件,等腰梯形的条件,分别求P点坐标,判断是否存在.
(1)B(﹣1,0)E(0,4)C(4,0)设解析式是y=ax2+bx+c,
可得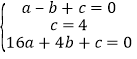 ,
,
解得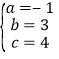 ,
,
∴y=﹣x2+3x+4;
(2)△BDC是直角三角形,
∵BD2=BO2+DO2=5,DC2=DO2+CO2=20,BC2=(BO+CO)2=25
∴BD2+DC2=BC2,
∴△BDC是直角三角形.
点A坐标是(﹣2,0),点D坐标是(0,2),
设直线AD的解析式是y=kx+b,则![]() ,
,
解得:![]() ,
,
则直线AD的解析式是y=x+2,
设点P坐标是(x,x+2)
当OP=OC时x2+(x+2)2=16,
解得:x=﹣1±![]() (x=﹣1-
(x=﹣1-![]() (不符合,舍去)此时点P(﹣1+
(不符合,舍去)此时点P(﹣1+![]() ,1+
,1+![]() )
)
当PC=OC时(x+2)2+(4﹣x)2=16,方程无解;
当PO=PC时,点P在OC的中垂线上,
∴点P横坐标是2,得点P坐标是(2,4);
∴当△POC是等腰三角形时,点P坐标是(﹣1+![]() ,1+
,1+![]() )或(2,4);
)或(2,4);
(3)点M坐标是(![]() ,
,![]() ),点N坐标是(
),点N坐标是(![]() ,
,![]() ),∴MN=
),∴MN=![]() ,
,
设点P为(x,x+2),Q(x,﹣x2+3x+4),则PQ=﹣x2+2x+2
①若PQNM是菱形,则PQ=MN,可得x1=0.5,x2=1.5
当x2=1.5时,点P与点M重合;当x1=0.5时,可求得PM=![]() 所以菱形不存在.
所以菱形不存在.
②能成为等腰梯形,作QH⊥MN于点H,作PJ⊥MN于点J,则NH=MJ,
则![]() ﹣(﹣x2+3x+4)=x+2﹣
﹣(﹣x2+3x+4)=x+2﹣![]() ,
,
解得:x=2.5,
此时点P的坐标是(2.5,4.5).


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题:
已知A、B两地相距48千米,甲骑自行车每小时走18千米,乙步行每小时走6千米,甲乙两人分别A、B两地同时出发.
(1)同向而行,开始时乙在前,经过多少小时甲追上乙?
(2)相向而行,经过多少小时两人相距40千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能灯在城市已经基本普及,某商场计划购进甲、乙两种型号的节能灯共1200只,这两种节能灯的进价、售价如下表:
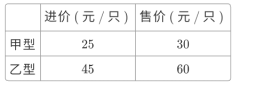
(1)如何进货,进货款恰好为46000元.
(2)如何进货,商场销售完节能灯后获利恰好是进货价的30%,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用正方形是墩垒石梯,下图分别表示垒到一、二阶梯时的情况,那么照这样垒下去
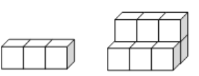
一级 二级
①填出下表中未填的两空,观察规律。
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 |
②到第n级阶梯时,共用正方体石墩_______________块(用n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:
点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.
当A,B两点中有一点在原点时,不妨设点A在原点,如图(1),|AB|=|OB|=|b|=|a﹣b|;当A,B两点都不在原点时,
①如图(2),点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图(3),点A,B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图(4),点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|;
综上,数轴上A,B两点之间的距离|AB|=|a﹣b|.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③当代数式|x+1|+|x﹣2|取最小值时,相应的x的取值范围是 .
④解方程|x+1|+|x﹣2|=5.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:
依此估计此封闭图形ABC的面积是_____m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线.ON是∠BOC的平分线.
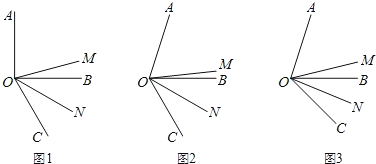
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果)
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON﹣∠CON= (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣![]() ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com