
 ��ͼ����ƽ��ֱ������ϵxoy�У�����ABCD�ı�AB��x���ϣ���AB=3��BC=2$\sqrt{3}$��ֱ��y=$\sqrt{3}$x-2$\sqrt{3}$������C����y���ڵ�G��
��ͼ����ƽ��ֱ������ϵxoy�У�����ABCD�ı�AB��x���ϣ���AB=3��BC=2$\sqrt{3}$��ֱ��y=$\sqrt{3}$x-2$\sqrt{3}$������C����y���ڵ�G������ ��1������y=2$\sqrt{3}$���x��ֵ���ʿɵó�OA�ij������������ε����ʼ��ɵó�C��D�����ꣻ
��2���ɶ��κ����Գ��Եó��䶥�����꣬�������߽���ʽΪy=a��x-$\frac{5}{2}$��2+$\frac{\sqrt{3}}{2}$���ѵ�D��1��2$\sqrt{3}$���������a��ֵ���ʿɵó����κ����Ľ���ʽ���ó���M�����꣮���ô���ϵ�������ֱ��CM�Ľ���ʽ���ٸ��������ε�������ɵó����ۣ�
��3���趥��E��ֱ�����˶��ĺ�����Ϊm����E��m��$\sqrt{3}$m-2$\sqrt{3}$����m��0�����ʿ������ʽΪy=$\frac{2\sqrt{3}}{3}$��x-m��2+$\sqrt{3}$m-2���ٷ�FG=EG��GE=EF��FG=FE��������������ۣ�
��� �⣺��1����y=2$\sqrt{3}$��2$\sqrt{3}$=$\sqrt{3}$x-2$\sqrt{3}$�����x=4��
��OA=4-3=1��
��C��4��2$\sqrt{3}$����D��1��2$\sqrt{3}$����
��2���ɶ��κ����Գ��Եã����������Ϊ$\frac{1+4}{2}$=$\frac{5}{2}$��
��x=$\frac{5}{2}$����y=$\sqrt{3}$��$\frac{5}{2}$-2$\sqrt{3}$=$\frac{\sqrt{3}}{2}$��
�ඥ������Ϊ��$\frac{5}{2}$��$\frac{\sqrt{3}}{2}$����
���������߽���ʽΪy=a��x-$\frac{5}{2}$��2+$\frac{\sqrt{3}}{2}$���ѵ�D��1��2$\sqrt{3}$������ã�a=$\frac{2\sqrt{3}}{3}$��
�����ʽΪy=$\frac{2\sqrt{3}}{3}$��x-$\frac{5}{2}$��2+$\frac{\sqrt{3}}{2}$��
��$y=\frac{{2\sqrt{3}}}{3}{x^2}-\frac{{10\sqrt{3}}}{3}x+\frac{{14\sqrt{3}}}{3}$��
��M��0��$\frac{{14\sqrt{3}}}{3}$��
�֡�C��4��2$\sqrt{3}$����
��ֱ��CM�Ľ���ʽΪy=$-\frac{{2\sqrt{3}}}{3}x+\frac{{14\sqrt{3}}}{3}$
����Q��QH��x�ύֱ��CM�ڵ�H
��Q��m��$\frac{2\sqrt{3}}{3}$m2-$\frac{10\sqrt{3}}{3}$m+$\frac{14\sqrt{3}}{3}$������H��m��-$\frac{2\sqrt{3}}{3}$m+$\frac{14\sqrt{3}}{3}$��
��S��MCQ=$\frac{1}{2}QH��{{x_c}-{x_m}}��=2��{-\frac{{2\sqrt{3}}}{3}m+\frac{{14\sqrt{3}}}{3}-\frac{{2\sqrt{3}}}{3}{m^2}+\frac{{10\sqrt{3}}}{3}m-\frac{{14\sqrt{3}}}{3}}��$
=$-\frac{{4\sqrt{3}}}{3}{��{m-2}��^2}+\frac{{16\sqrt{3}}}{3}$
���Ե�m=2ʱ��S��MCQ���=$\frac{{16\sqrt{3}}}{3}$����ʱQ��2��$\frac{{2\sqrt{3}}}{3}$��
��3���趥��E��ֱ�����˶��ĺ�����Ϊm����E��m��$\sqrt{3}$m-2$\sqrt{3}$����m��0��
��������ʽΪy=$\frac{2\sqrt{3}}{3}$��x-m��2+$\sqrt{3}$m-2$\sqrt{3}$��
����FG=EGʱ��FG=EG=2m����F��0��2m-2$\sqrt{3}$����
�������ʽ��$\frac{2\sqrt{3}}{3}$m2+$\sqrt{3}$m-2$\sqrt{3}$=2m-2$\sqrt{3}$��
��m=0����ȥ����m=$\sqrt{3}$-$\frac{3}{2}$��
��ʱ����Ľ���ʽΪ��y=$\frac{2\sqrt{3}}{3}$��x-$\sqrt{3}$+$\frac{3}{2}$��2+3-$\frac{7\sqrt{3}}{2}$��
����GE=EFʱ��FG=2$\sqrt{3}$m����F��0��2$\sqrt{3}$m-2$\sqrt{3}$����
�������ʽ�ã�$\frac{2\sqrt{3}}{3}$m2+$\sqrt{3}$m-2$\sqrt{3}$=2$\sqrt{3}$m-2$\sqrt{3}$�����m=0����ȥ����m=$\frac{3}{2}$��
��ʱ����Ľ���ʽΪ��y=$\frac{2\sqrt{3}}{3}$��x-$\frac{3}{2}$��2-$\frac{\sqrt{3}}{2}$��
����FG=FEʱ��
��ƽ�ƺ������ߵĶ�����y���Ҳ࣬
���GEFΪ�۽ǣ�
�������������ڣ�
���� ���⿼����Ƕ��κ����ۺ��⣬�漰����ԳƵ����ʡ����κ���ͼ���ϵ�������ص��֪ʶ���ѶȽϴ�


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
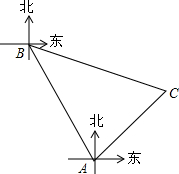 ij������A��B�����ۿڣ�B�ۿ���A�ۿڱ�ƫ��30�㷽���ϣ���A�ۿ�60�����һ�Ҵ���A�ۿڳ������ض���������ʻһ�ξ������λ��B�ۿ���ƫ��75�㷽���C������ô���B�ۿ�֮��ľ��뼴CB�ij�������������ţ���
ij������A��B�����ۿڣ�B�ۿ���A�ۿڱ�ƫ��30�㷽���ϣ���A�ۿ�60�����һ�Ҵ���A�ۿڳ������ض���������ʻһ�ξ������λ��B�ۿ���ƫ��75�㷽���C������ô���B�ۿ�֮��ľ��뼴CB�ij�������������ţ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com