
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?

【答案】(1)点A坐标为(1,4),y=﹣x2+2x+3;(2)当t=![]() 或t=
或t=![]() 时,△PCQ为直角三角形;(3)当t=2时,△ACQ的面积最大,最大值是1.
时,△PCQ为直角三角形;(3)当t=2时,△ACQ的面积最大,最大值是1.
【解析】试题分析:(1)根据矩形的三个顶点坐标以及抛物线的对称轴可求出点A的坐标;设抛物线的解析式为顶点式,然后把点A、C坐标代入计算即可;(2)分∠QPC=90°和∠PQC=90°两种情况讨论,利用比例线段可求出t的值;(3)求出直线AC的解析式,然后把点P(1,4﹣t)的纵坐标代入,然后用t可表示出点Q的坐标,以及QF的长,然后可求出△ACQ的面积与t的函数关系式,利用二次函数的性质确定函数值的值即可.
试题解析:解:(1)∵抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,
∴点A坐标为(1,4),
设抛物线的解析式为y=a(x﹣1)2+4,
把C(3,0)代入抛物线的解析式,可得a(3﹣1)2+4=0,
解得a=﹣1.
故抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(2)依题意有:OC=3,OE=4,
∴CE=![]() =
=![]() =5,
=5,
当∠QPC=90°时,
∵cos∠QPC=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() ;
;
当∠PQC=90°时,
∵cos∠QCP=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() .
.
∴当t=![]() 或t=
或t=![]() 时,△PCQ为直角三角形;
时,△PCQ为直角三角形;
(3)∵A(1,4),C(3,0),
设直线AC的解析式为y=kx+b,则
![]() ,
,
解得![]() .
.
故直线AC的解析式为y=﹣2x+6.
∵P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得x=1+![]() ,
,
∴Q点的横坐标为1+![]() ,
,
将x=1+![]() 代入y=﹣(x﹣1)2+4中,得y=4﹣
代入y=﹣(x﹣1)2+4中,得y=4﹣![]() .
.
∴Q点的纵坐标为4﹣![]() ,
,
∴QF=(4﹣![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣![]() ,
,
∴S△ACQ=S△AFQ+S△CPQ
=![]() FQAG+
FQAG+![]() FQDG
FQDG
=![]() FQ(AG+DG)
FQ(AG+DG)
=![]() FQAD
FQAD
=![]() ×2(t﹣
×2(t﹣![]() )
)
=﹣![]() (t﹣2)2+1,
(t﹣2)2+1,
∴当t=2时,△ACQ的面积最大,最大值是1.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
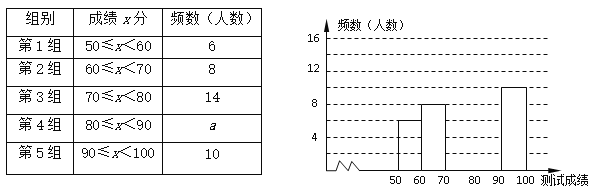
请结合图表完成下列各题:
(1)①表中a的值为 ; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:
(1)若从中抽出2张卡片,且这2个数字的差最小,应如何抽取?最小值是多少?
(2)若从中抽出2张卡片,且这2个数字的积最大,应如何抽取?最小值是多少?
(3)若从中抽出4张卡片,运用加、减、乘、除、乘方、括号等运算符号,使得结果为24.请写出运算式.(只需写出一种)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长沙市现在常住人口大约有732万,数据732万用科学记数法表示为( )
A.732×104B.73.2×105C.7.32×106D.0.732×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线y= ![]() x﹣4与x轴,y轴分别交于B、A,将该直线绕A点顺时针旋转α,且tanα=
x﹣4与x轴,y轴分别交于B、A,将该直线绕A点顺时针旋转α,且tanα= ![]() ,旋转后与x轴交于C点.
,旋转后与x轴交于C点.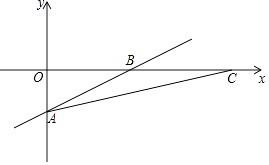
(1)求A、B、C的坐标;
(2)在x轴上找一点P,使有一动点能在最短的时间内从点A出发,沿着A﹣P﹣C的运动到达C点,并且在AP上以每秒2个单位的速度移动,在PC上以每秒 ![]() 个单位移动,试用尺规作图找到P点的位置(不写作法,保留作图痕迹),并求出所用的最短时间t.
个单位移动,试用尺规作图找到P点的位置(不写作法,保留作图痕迹),并求出所用的最短时间t.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com