
【题目】如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒). 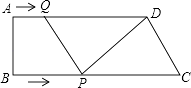
(1)当t为何值时,四边形PQDC是平行四边形.
(2)当t为何值时,以C、D、Q、P为顶点的梯形面积等于60cm2?
【答案】
(1)解:∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,如图1:

∵DQ=AD﹣AQ=16﹣t,
CP=21﹣2t
∴16﹣t=21﹣2t
解得:t=5
当P从C运动到B时,
∵DQ=AD﹣AQ=16﹣t,
CP=2t﹣21
∴16﹣t=2t﹣21,
解得:t= ![]() ,
,
∴当t=5或 ![]() 秒时,四边形PQDC是平行四边形
秒时,四边形PQDC是平行四边形
(2)解:若点P、Q分别沿AD、BC运动时,如图2:

![]() ×AB=60,
×AB=60,
即 ![]() ×12=60,
×12=60,
解得:t=9;
若点P返回时,CP=2(t﹣ ![]() ),
),
则  ×12=60,
×12=60,
解得:t=15.
故当t=9或15秒时,以C,D,Q,P为顶点的梯形面积等60cm2
【解析】(1)由题意已知,AD∥BC,要使四边形PQDC是平行四边形,则只需要让QD=PC即可,因为Q、P点的速度已知,AD、BC的长度已知,要求时间,用时间=路程÷速度,即可求出时间;(2)要使以C、D、Q、P为顶点的梯形面积等于60cm2,可以分为两种情况:点P、Q分别沿AD、BC运动或点P返回时,再利用梯形面积公式,即(QD+PC)×AB÷2=60,因为Q、P点的速度已知,AD、AB、BC的长度已知,用t可分别表示QD、BC的长,即可求得时间t.
【考点精析】利用平行四边形的判定与性质和梯形的定义对题目进行判断即可得到答案,需要熟知若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形.


科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5μm(0.0000025m)的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物.将0.0000025用科学记数法表示为( )
A.25×10﹣7
B.2.5×10﹣6
C.0.25×10﹣5
D.2.5×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点M(14,0)是x轴上的点,点P的坐标是(9,12),连接OP,PM. 
(1)求线段PM的长;
(2)在第一象限内找一点N,使四边形OPNM是平行四边形,画出图形并求出点N的坐标(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续正整数按如下个规律排列
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ……… | |
第一行 | 1 | 2 | 3 | 4 | ||
第二行 | 8 | 7 | 6 | 5 | ||
第三行 | 9 | 10 | 11 | 12 | ||
第四行 | 16 | 15 | 14 | 13 | ||
第五行 | 17 | 18 | 19 | 20 | ||
……… |
若正整数2019位于第a行、第b列,则a+b=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )

A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下: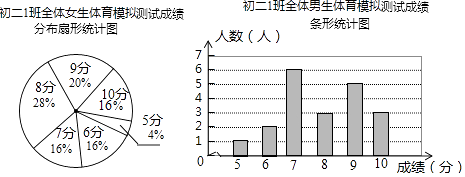
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根据以上信息,解答下列问题:
(1)这个班共有男生人,共有女生人;
(2)补全初二1班体育模拟测试成绩分析表;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE. 
(1)求证:AE=BD;
(2)求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三,股四,弦五”.它被记载于我国古代著名数学著作《周髀算经》中.为了方便,在本题中,我们把三边的比为3:4:5的三角形称为(3,4,5)型三角形.例如:三边长分别为9,12,15或![]() 的三角形就是(3,4,5)型三角形.用矩形纸片按下面的操作方法可以折出这种类型的三角形.
的三角形就是(3,4,5)型三角形.用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图1,在矩形纸片ABCD中,AD=8cm,AB=12cm.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.

问题解决
(1)请在图2中证明四边形AEFD是正方形.
(2)请在图4中判断NF与ND′的数量关系,并加以证明.
(3)请在图4中证明△AEN是(3,4,5)型三角形.
探索发现
(4)在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,联结OA、OC.
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离;
(3)记△AOB、△AOD、△COD 的面积分别为S1、S2、S3,如果S2是S1和S3的比例中项,求OD的长.
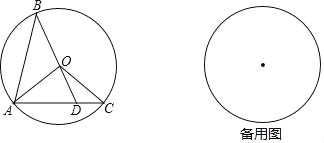
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com