
 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )| A. | $\sqrt{12}$ | B. | $\sqrt{10}$ | C. | $\sqrt{8}$ | D. | $\sqrt{6}$ |
分析 根据直角三角形斜边上的中线的性质可得DG=AG,根据等腰三角形的性质可得∠GAD=∠GDA,根据三角形外角的性质可得∠CGD=2∠GAD,再根据平行线的性质和等量关系可得∠ACD=∠CGD,根据等腰三角形的性质可得CD=DG,再根据勾股定理即可求解.
解答 解:∵AD∥BC,DE⊥BC,
∴AD⊥DE,
∵G为AF的中点,即DG为斜边AF的中线,
∴DG=AG=FG=3,
∴∠GAD=∠GDA,
∵AD∥BC,
∴∠GAD=∠ACB,
设∠ACB=α,则∠ACD=2α,
∵∠GAD=∠GDA=α,
∴∠DGC=2α,即∠ACD=∠DGC,
∴DG=DC=3,
在Rt△DEC中,DC=3,EC=1,
根据勾股定理得:DE=$\sqrt{D{C}^{2}-E{C}^{2}}$=$\sqrt{8}$,
故选C.
点评 本题考查了勾股定理,直角三角形斜边上中线性质,直角三角形的性质的应用,平行线的性质,解此题的关键是证出DG=DC.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:填空题
观察下面的图形(每个正方形的边长均为1)和相应的等式,探究其中的规律:
①
 1×
1× =1-
=1-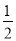
②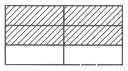
 2×
2×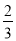 =2-
=2-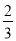
③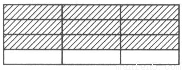
 3×
3×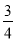 =3-
=3-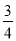
……
(1)在下面给出的四个正方形中画出第四个图形,并在右边写出与之对应的等式;

 _______________
_______________
(2)猜想并写出与第几个图形相对应的等式:______________________________。
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )| A. | a=c | B. | 当a=b=c时,四边形BEDF是菱形 | ||
| C. | $\frac{AF}{AB}$=$\frac{a}{a+b}$ | D. | 正方形ABCD面积为(a+b)2+c2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
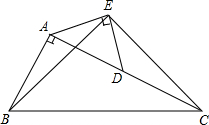 已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.
已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在等腰直角三角形ABC中,∠CAB=90°,以AB为边向外作等边△ABD,AE⊥BD,CD、AE交于点M,若DM=1,求BC的值.
如图,已知在等腰直角三角形ABC中,∠CAB=90°,以AB为边向外作等边△ABD,AE⊥BD,CD、AE交于点M,若DM=1,求BC的值.查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
如图所示,用量角器度量一些角的度数。下列结论中正确的是( )
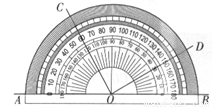
A. ∠BOC=60° B. ∠COD=150°
C. ∠AOC与∠BOD的大小相等 D. ∠AOC与∠BOD互余
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com