
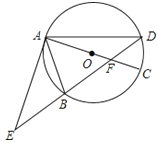
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、AE=4![]()
【解析】
试题分析:(1)、连接CD,根据直径所对的圆周角为直角得出∠ADB+∠EDC=90°,根据同弧所对的圆周角相等得出∠BAC=∠EDC,然后结合已知条件得出∠EAB+∠BAC=90°,从而说明切线;(2)、连接BC,根据直径的性质得出∠ABC=90°,根据B是EF的中点得出AB=EF,即∠BAC=∠AFE,则得出三角形相似;(3)、根据三角形相似得出![]() ,根据AF和CF的长度得出AC的长度,然后根据EF=2AB代入
,根据AF和CF的长度得出AC的长度,然后根据EF=2AB代入![]() 求出AB和EF的长度,最后根据Rt△AEF的勾股定理求出AE的长度.
求出AB和EF的长度,最后根据Rt△AEF的勾股定理求出AE的长度.
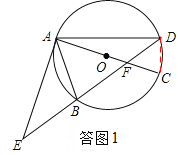
试题解析:(1)、如答图1,连接CD, ∵AC是⊙O的直径,∴∠ADC=90°. ∴∠ADB+∠EDC=90°.
∵∠BAC=∠EDC,∠EAB=∠ADB, ∴∠BAC=∠EAB+∠BAC=90°. ∴EA是⊙O的切线.
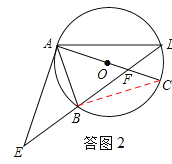
(2)、如答图2,连接BC, ∵AC是⊙O的直径,∴∠ABC=90°. ∴∠CBA=∠ABC=90°.
∵B是EF的中点,∴在Rt△EAF中,AB=BF. ∴∠BAC=∠AFE. ∴△EAF∽△CBA.
(3)、∵△EAF∽△CBA,∴![]() . ∵AF=4,CF=2, ∴AC=6,EF=2AB.
. ∵AF=4,CF=2, ∴AC=6,EF=2AB.
∴![]() ,解得AB=2
,解得AB=2![]() .∴EF=4
.∴EF=4![]() .
.
∴AE=![]() .
.


科目:初中数学 来源: 题型:
【题目】点(x1,y1)、(x2,y2)在直线y=﹣x+b上,若x1<x2,则y1与y2大小关系是( )
A. y1<y2 B. y1=y2 C. y1>y2 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据省统计局公布的数据,安徽省2019年第二季度GDP总值约为7.9千亿元人民币,若我省第四季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=7.9(1+2x)B.y=7.9(1-x)2
C.y=7.9(1+x)2D.y=7.9+7.9(1+x)+7.9(1+x)2
查看答案和解析>>
科目:初中数学 来源: 题型:
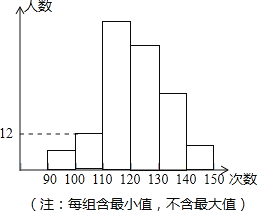
【题目】为了了解合肥市九年级毕业生的体能情况,合肥市随机抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如图统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
(1)第二小组的人数占这次抽调学生总数的百分之几?
(2)这次共抽调了多少人?
(3)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是 (在横线上直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
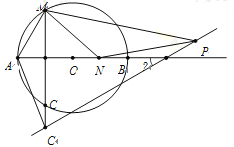
【题目】如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
(1)若AM=AC,点N与点O重合,则α= °;
(2)若点C、点N的位置如图所示,求α的度数;
(3)当直线PC与⊙O相切时,则MC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
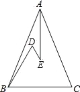
【题目】如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com