【题目】已知
，点
在
的内部，
，在
、
上分别取点
、
，使
的周长最短，则
周长的最小值为（ ）
A.4B.8C.16D.32
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案科目：初中数学 来源： 题型：
【题目】如图，将ABCD的AD边延长至点E，使DE＝
AD，连接CE，F是BC边的中点，连接FD．
(1)求证：四边形CEDF是平行四边形；
(2)若AB＝3，AD＝4，∠A＝60°，求CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
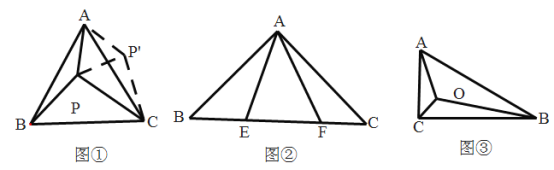
【题目】阅读理解题
（1）阅读理解：如图①，等边
内有一点
，若点到顶点
，
，
的距离分别为3，4，5，求
的大小.
思路点拨：考虑到
，
，
不在一个三角形中，采用转化与化归的数学思想，可以将
绕顶点逆时针旋转
到
处，此时
，这样，就可以利用全等三角形知识，结合已知条件，将三条线段的长度转化到一个三角形中，从而求出的度数.请你写出完整的解题过程.
（2）变式拓展：请你利用第（1）题的解答思想方法，解答下面问题：
已知如图②，中，
，
，
、
为
上的点且
，
，
，求
的大小.
（3）能力提升：如图③，在
中，
，
，
，点
为内一点，连接
，
，
，且
，请直接写出
的值，即
______.
查看答案和解析>>
科目：初中数学 来源： 题型：
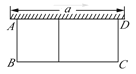
【题目】如图，有一个长为24米的篱笆，一面利用墙（墙的最大长度a为15米）围成的中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S平方米．
（1）求S与x的函数关系式；
（2）如果要使围成花圃面积最大，求AB的长为多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
中，
厘米，
厘米，点
为
的中点．
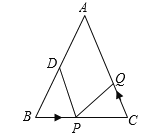
（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1秒后，
与
是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等， 与是否可能全等？若能，求出全等时点Q的运动速度和时间；若不能，请说明理由．
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿三边运动，求经过多长时间点P与点Q第一次在的哪条边上相遇？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图在直角坐标系中，点A在y轴上，BC⊥x轴于点C，点A关于直线OB的对称点D恰好在BC上，点E与点O关于直线BC对称，∠OBC=35°，则∠OED的度数为（ ）
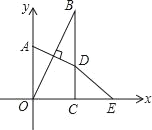
A.10°B.20°C.30°D.35°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点．
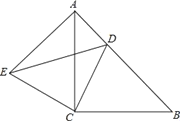
（1）求证：△BCD≌△ACE；
（2）若AD=3，BD=4，求DE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
