
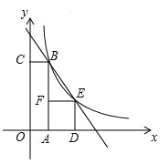
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F在AB上,点B,E是双曲线y1=![]() 与直线y2=mx+n的交点,OA=2,OC=6.
与直线y2=mx+n的交点,OA=2,OC=6.
(1)求k的值;
(2)求正方形ADEF的边长;
(3)直接写出不等式![]() >mx+n的解集.
>mx+n的解集.
【答案】(1)k=12;(2)![]() ;(3)0<x<2或x>
;(3)0<x<2或x>![]()
【解析】
(1)根据OA=2,OC=6, 可得点B坐标为(2,6),代入反比例函数的解析式即可解答;(2)由(1)解得反比例函数解析式为y=![]() ,设AD=t,则OD=2+t,所以E点坐标为(2+t,t),再根据反比例函数图象上点的坐标特征得(2+t)t=12,利用因式分解法可求出t的值;(3)反比例函数的函数值大于一次函数,即对应相同的x的值时,一反比例函数对应的点在一次函数的图象的点的上边,据此即可判断.
,设AD=t,则OD=2+t,所以E点坐标为(2+t,t),再根据反比例函数图象上点的坐标特征得(2+t)t=12,利用因式分解法可求出t的值;(3)反比例函数的函数值大于一次函数,即对应相同的x的值时,一反比例函数对应的点在一次函数的图象的点的上边,据此即可判断.
解:(1)∵OA=2,OC=6, ∴点B坐标为(2,6)
∴ ![]() ,∴k=12;
,∴k=12;
(2)设正方形边长为a,则点E坐标为(a+2,a),
∴a(a+2)=12,解得:a=![]() ,
,
又a>0,∴a=![]() ;
;
(3)不等式![]() >mx+n的解集是:0<x<2或x>
>mx+n的解集是:0<x<2或x>![]()


科目:初中数学 来源: 题型:
【题目】(本题10分)如图,直线y=x+m和抛物线y=![]() +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),
B(3,2).

(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
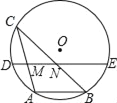
【题目】如图,⊙O的弦AB=4cm,点C为优弧![]() 上的动点,且∠ACB=30°.若弦DE经过弦AC、BC的中点M、N,则DM+EN的最大值是_____cm.
上的动点,且∠ACB=30°.若弦DE经过弦AC、BC的中点M、N,则DM+EN的最大值是_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=5,BC=8,点E为AD上一个动点,把△ABE沿BE折叠,点A的对应点为点F,连接DF,连接CF.当点F落在矩形内部,且CF=CD时,AE的长为( ).
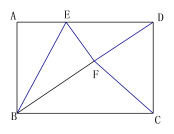
A. 3B. 2.5C. 2D. 1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
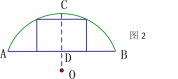
【题目】如图,某地有一座圆弧形拱桥,
(1)如图1,请用尺规作出圆弧所在圆的圆心O;
![]()
(2)如图2,过点O作OC⊥AB于点D,交圆弧于点C,CD=2.4 m.桥下水面宽度AB为7.2 m,现有一艘宽3 m、船舱顶部为方形并高出水面2 m的货船要经过拱桥,请通过计算说明此货船能否顺利通过这座拱桥.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把(sinα)2记作sin2α,根据图1和图2完成下列各题.
(1)sin2A1+cos2A1= ,sin2A2+cos2A2= ,sin2A3+cos2A3= ;
(2)观察上述等式猜想:在Rt△ABC中,∠C=90°,总有sin2A+cos2A= ;
(3)如图2,在Rt△ABC中证明(2)题中的猜想:
(4)已知在△ABC中,∠A+∠B=90°,且sinA=![]() ,求cosA.
,求cosA.

查看答案和解析>>
科目:初中数学 来源: 题型:
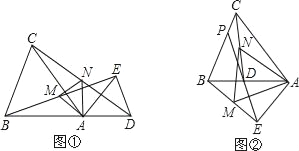
【题目】已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.
(1)求证:①BE=CD;②△AMN是等腰三角形;
(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;
(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.
查看答案和解析>>
科目:初中数学 来源: 题型:
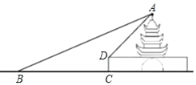
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com