
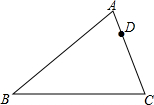
 如图,已知在△ABC中,AB=14,BC=12,AC=10,D是AC上一点,且AD=4,过点D画一条直线l,把△ABC分成两部分,使其中的一个三角形与△ABC相似,请在图中画出所有符合要求的直线l,并写出所作三角形与△ABC的相似比.
如图,已知在△ABC中,AB=14,BC=12,AC=10,D是AC上一点,且AD=4,过点D画一条直线l,把△ABC分成两部分,使其中的一个三角形与△ABC相似,请在图中画出所有符合要求的直线l,并写出所作三角形与△ABC的相似比. 分析 分别利用当DF∥BC时,当∠ADE=∠B时,当DN∥AB时,当∠CDM=∠B时求出相似三角形,进而得出相似比.
解答  解:如图所示:当DF∥BC时,则△AFD∽△ABC,
解:如图所示:当DF∥BC时,则△AFD∽△ABC,
故△AFD与△ABC的相似比为:$\frac{AD}{AC}$=$\frac{4}{10}$=$\frac{2}{5}$;
当∠ADE=∠B时,则△ADE∽△ABC,
故△ADE与△ABC的相似比为:$\frac{AD}{AB}$=$\frac{2}{7}$;
当DN∥AB时,则△CDN∽△CAB,
故△CDN与△CAB的相似比为:$\frac{CD}{AC}$=$\frac{10-4}{10}$=$\frac{3}{5}$;
当∠CDM=∠B时,则△CDM∽△CBA,
故△CDM与△CBA的相似比为:$\frac{CD}{BC}$=$\frac{6}{12}$=$\frac{1}{2}$.
点评 此题主要考查了相似变换,利用分类讨论得出相似三角形是解题关键,注意不要漏解.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
 如图所示为某汽车行驶的路程S(km)与时间t(min)的函数关系图,观察图中所提供的信息解答下列问题:
如图所示为某汽车行驶的路程S(km)与时间t(min)的函数关系图,观察图中所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上表示的是一个不等式的解集,则这个不等式组可能是( )
如图,数轴上表示的是一个不等式的解集,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}{y≥-1}\\{x<2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≤-1}\\{x>2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x<-1}\\{x≥2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x>-1}\\{x≤2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC的三个顶点的坐标分别为A(4,6),B(-4,2),C(-2,0).
如图,已知△ABC的三个顶点的坐标分别为A(4,6),B(-4,2),C(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形网格上有一个△DEF.
如图,在正方形网格上有一个△DEF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com