
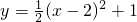 ,当x________时,y随x的增大而增大.
,当x________时,y随x的增大而增大. 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
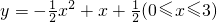 ,当x=______时,y取最大值是______;当x=______时,y取最小值是______.
,当x=______时,y取最大值是______;当x=______时,y取最小值是______.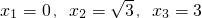 ,对应的值y分别是y1、y2、y3,则y1、y2、y3的大小关系是______.
,对应的值y分别是y1、y2、y3,则y1、y2、y3的大小关系是______.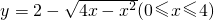 的最大值与最小值分别是______.
的最大值与最小值分别是______.查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线![]() .
.
⑴当a =-1时,求此抛物线的顶点坐标和对称轴;
⑵若代数式![]() 的值为正整数,求x的值;
的值为正整数,求x的值;
⑶当![]() 时,抛物线
时,抛物线![]() 与x轴的正半轴相交于点M(m,0);当
与x轴的正半轴相交于点M(m,0);当![]() 时,抛物线
时,抛物线![]() 与x轴的正半轴交于点N(n,0).若点M在点N的左边,试比较
与x轴的正半轴交于点N(n,0).若点M在点N的左边,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源:竞赛辅导:二次函数的最值问题(解析版) 题型:填空题
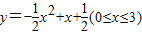 ,当x= 时,y取最大值是 ;当x= 时,y取最小值是 .
,当x= 时,y取最大值是 ;当x= 时,y取最小值是 .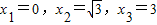 ,对应的值y分别是y1、y2、y3,则y1、y2、y3的大小关系是 .
,对应的值y分别是y1、y2、y3,则y1、y2、y3的大小关系是 .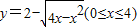 的最大值与最小值分别是 .
的最大值与最小值分别是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com