【题目】某商店欲购进
两种商品，已知购进
种商品5件和
种商品4件共需300元；若购进种商品6件和种商品8件共需440元；
（1）求两种商品每件的进价分别为多少元？
（2）若该商店，种商品每件的售价为48元，种商品每件的售价为31元，且商店将购进共50件的商品全部售出后，要获得的利润超过348元，求种商品至少购进多少件？
【答案】（1）A种商品进价为40元，B种商品进价为25元；（2）至少购进A种商品25件．
【解析】
（1）设A种商品进价为x元，B种商品进价为y元．由购进A种商品5件和B种商品4件需300元和购进A种商品6件和B种商品8件需440元建立方程组，求解即可；
（2）设购进A种商品a件，则购进B种商品（50a）件，根据获得的利润超过348元，建立不等式求解即可．
解：（1）设A种商品进价为x元，B种商品进价为y元，
由题意，得：
，
解得：
，
答：A种商品进价为40元，B种商品进价为25元；
（2）设购进A种商品a件，则购进B种商品（50a）件，
由题意，得：
，
解得：a＞24，
∴a取25，
答：至少购进A种商品25件．
习题精选系列答案科目：初中数学 来源： 题型：
【题目】如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫做格点．△ABC的顶点在格点上，A（1，0）、C（0，7）．
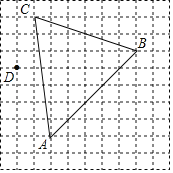
（1）在方格纸中画出平面直角坐标系，写出B点的坐标：B ；
（2）直接写出△ABC的形状： ，直接写出△ABC的面积 ；
（3）若D（﹣1，4），连接BD交AC于E，则
＝ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（问题实验）如图①，在地面
上有两根等长立柱
，
之间悬挂一根近似成抛物线
的绳子．
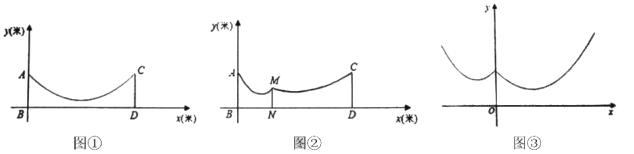
（1）求绳子最低点到地面的距离；
（2）如图②，因实际需要，需用一根立柱
撑起绳子．
①若在离为4米的位置处用立柱撑起，使立柱左侧的抛物线的最低点距为1米，离地面1.8米，求的长；
②将立柱来回移动，移动过程中，在一定范围内，总保持立柱左侧抛物线的形状不变，其函数表达式为
，当抛物线最低点到地面距离为0.5米时，求
的值．
（问题抽象）如图③，在平面直角坐标系中，函数
的图像记为
，函数
的图像记为
，其中是常数，图像、合起来得到的图像记为
．
设在
上的最低点纵坐标为
，当
时，直接写出的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】课外兴趣小组为了解某段路上机动车的车速，抽查了一段时间内若干辆车的车速（车速取整数，单位：千米/时）并制成如图所示的频数分布直方图．已知车速在41千米/时到50千米/时的车辆数占车辆总数的
．
（1）在这段时间内他们抽查的车有 辆；
（2）被抽查车辆的车速的中位数所在速度段（单位：千米/时）是（ ）
A．30.5~40.5 B．40.5~50.5 C．50.5~60.5 D．60.5~70.5
（3）补全频数分布直方图；
（4）如果全天超速（车速大于60千米/时）的车有200辆，则当天的车流量约为多少辆？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两台机床同时加工一批直径为100毫米的零件，为了检验产品的质量，从产品中随机抽查6件进行测量，测得的数据如下：（单位：毫米）甲机床：99 98 100 100 103乙机床：99 100 102 99 100 100则加工这批零件性能较好的机床是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
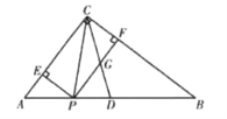
【题目】如图，在
中，
为斜边
中点，点P从A出发，沿以每秒5个单位的速度向终点B运动，过点P作
于F，得到矩形
与矩形
的一边交于点G，连接PC，设点P的运动时间为
秒．
（1）求线段
的长（用含的代数式表示）；
（2）当
时，求线段
多长；
（3）当点P不与
重合时，设矩形与三角形CPD重叠部分图形的面积是
，求与之间的函数关系式；
（4）在点P出发的同时，点Q从点D出发，沿
以每秒6个单位的速度向终点D移动，当点Q在矩形内部时，直接写出的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小楠是一个乐学习，善思考，爱探究的同学，她对函数
的图象和性质进行了探究，请你将下列探究过程补充完整：
（1）函数的自变量
的取值范围是________________；
（2）用描点法画函数图象：
①列表：
| … | -5 | -2 | -1 | 0 | … | 2 | 3 | 4 | 7 | … |
| … |
| 2 | 3 |
| … | 6 | 3 | 2 | 1 | … |
表中
的值为______________，
的值为_______________．
②描点连线：请在右图画出该图象的另一部分．
（3）观察函数图象，得到函数的性质之一：当_____________时，函数值
随的增大而增大．
（4）应用：若
，则的取值范围是______________．
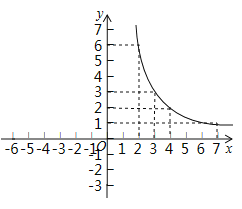
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O的直径AB＝26，P是AB上(不与点A、B重合)的任一点，点C、D为⊙O上的两点，若∠APD＝∠BPC，则称∠CPD为直径AB的“回旋角”．
(1)若∠BPC＝∠DPC＝60°，则∠CPD是直径AB的“回旋角”吗？并说明理由；
(2)若
的长为
π，求“回旋角”∠CPD的度数；
(3)若直径AB的“回旋角”为120°，且△PCD的周长为24+13
，直接写出AP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知A（
，y1），B(2,y2)为反比例函数
图像上的两点，动点P(x，0)在x正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）
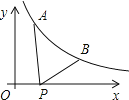
A. (，0) B. (1,0) C. (
,0) D. (
,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com