某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施．调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．
（1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）
（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？
（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？
解：（1）根据题意，得y=（2400﹣2000﹣x）（8+4×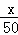
），
即y=﹣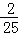
x2+24x+3200；
（2）由题意，得﹣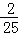x2+24x+3200=4800．
整理，得x2﹣300x+20000=0．
解这个方程，得x1=100，x2=200．
要使百姓得到实惠，取x=200元．
∴每台冰箱应降价200元；
（3）对于y=﹣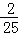x2+24x+3200=﹣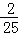（x﹣150）2+5000，
当x=150时，
y最大值=5000（元）．
所以，每台冰箱的售价降价150元时，商场的利润最大，最大利润是5000元．
点评： 求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法．借助二次函数解决实际问题．
科目：初中数学 来源： 题型：
端午节
吃粽子是中华民族的传统习俗，五月初五早上，奶奶为小明准备了四只粽子：一
只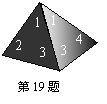
肉馅，一只香肠馅，两只红枣馅，四只粽子除内部馅料不同外其他均一切相同。小明喜欢
吃红枣馅的粽子。
（1）请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率；
（2）在吃粽子之前，小明准备用一格均匀的正四面体骰子（如图所示）
进行吃粽子的模拟试验，规定：掷得点数1向上代表肉馅，点数2向上代
表香肠馅，点数3，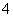
向上代表红枣馅，连续抛掷
这个骰子两次表示随机
吃两只粽子，从而估计吃两只粽子刚好都是红枣馅的概率。你认为这样模拟正确吗？试说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
若抛物线y=（m﹣1）x2+2mx+3m﹣2的顶点在坐标轴上，则m的值为 0或0.5或2 ．
考点： 二次函数的性质；二次函数的定义．
分析： 由于抛物线的顶点在坐标轴上，故应分在x轴上与y轴上两种情况进行讨论．
解答： 解：①当抛物线y=（m﹣1）2x2+2mx+3m﹣2的顶点在x轴上时，△=0，m﹣1≠0，
△=（2m）2﹣4×（m﹣1）×（3m﹣2）=0，
整理，得2m2﹣5m+2=0，
解得m=0.5或2；
②当抛物线y=（m﹣1）2x2+2mx+3m﹣2的顶点在y轴上时，
x=﹣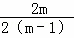
=﹣
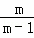=0，
解得m=0．
故答案为：0或0.5或2．
点评： 本题考查的是二次函数的性质，解答此题时要注意进行分类讨论，不要漏解．
查看答案和解析>>
科目：初中数学 来源： 题型：
抛物线y=x2+bx+c过点（2，﹣2）和（﹣1，10），与x轴交于A、B两点，与y轴交于C点．
（1）求抛物线的解析式．
（2）求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
| |
A．20° B．24° C．25° D．26°
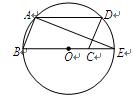
查看答案和解析>>
科目：初中数学 来源： 题型：
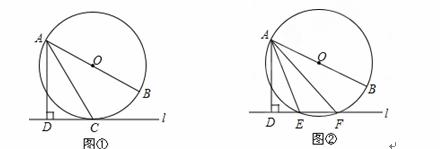
已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．
（1）如图①，当直线l与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；
（2）如图②，当直线l与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
B．— 
；②
；③
；④
.按此规律
，第五个方程的两个根为（ ）