
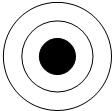
 如图,如图,有三个同心圆,由里向外的半径依次是2cm,4cm,6cm将圆盘分为三部分,飞镖可以落
如图,如图,有三个同心圆,由里向外的半径依次是2cm,4cm,6cm将圆盘分为三部分,飞镖可以落



 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
| 2 |
| x |
| 1 |
| x |
| 2 |
| x |
| 1 |
| x |
| 2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
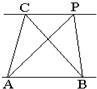 20、探究规律:如图,已知直线m∥n,A,B为直线n上的两点,C,P为直线m上的两点.如果A,B,C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有
20、探究规律:如图,已知直线m∥n,A,B为直线n上的两点,C,P为直线m上的两点.如果A,B,C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有查看答案和解析>>
科目:初中数学 来源: 题型:
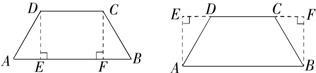
查看答案和解析>>
科目:初中数学 来源: 题型:
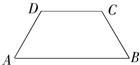
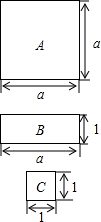 如图,有A型、B型、C型三种不同的纸板,其中
如图,有A型、B型、C型三种不同的纸板,其中查看答案和解析>>
科目:初中数学 来源: 题型:
如右图,有三个大小一样的正方体,每个正方体的六个面上都按 照相同的顺序,依次标有1,2,3,4,5,6这六个数字,并且把标有“6”的面都放在左边,那么它们底面所标的3个数字之和等于( )
A、8 B、9 C、10 D、11

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com