
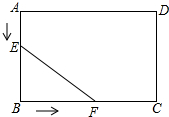
 如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.
如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.分析 (1)用t表示出BE及BF的长,再由三角形的面积公式即可得出结论;
(2)分△BEF∽△ABD与△BEF与△ADB两种情况进行讨论即可.
解答 解:(1)∵AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,
∴BE=5-t,BF=2t.
∵△BEF的面积为5cm2,
∴$\frac{1}{2}$BF•BE=5,即$\frac{1}{2}$×2t×(5-t)=5,解得t1=$\frac{5+\sqrt{5}}{2}$(舍去),t2=$\frac{5-\sqrt{5}}{2}$.
答:当t=$\frac{5-\sqrt{5}}{2}$时,△BEF的面积为5cm2;
(2)∵BE=5-t,BF=2t,
∴当△BEF∽△ABD时,$\frac{BE}{AB}$=$\frac{BF}{AD}$,即$\frac{5-t}{5}$=$\frac{2t}{7}$,解得t=$\frac{35}{17}$;
当△BEF与△ADB时,$\frac{BE}{AD}$=$\frac{BF}{AB}$,即$\frac{5-t}{7}$=$\frac{2t}{5}$,解得t=$\frac{25}{19}$.
综上所述,当t为$\frac{35}{17}$秒或$\frac{25}{19}$秒时,BEF与△ABD相似.
点评 本题考查的是相似三角形的判定,在解答此题时要注意进行分类讨论,不要漏解.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
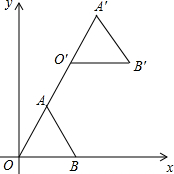 已知:如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内
已知:如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -3 | -8 | +14 | -10 | +15 | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com