
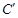 处,得折痕EF;
处,得折痕EF;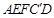 折叠,使AE、
折叠,使AE、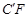 重合,得折痕DG,再打开;
重合,得折痕DG,再打开;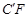 均落在DG上,点A、
均落在DG上,点A、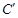 落在点
落在点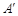 处,点E、F落在点
处,点E、F落在点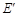 处,得折痕MN、QP.这样,就可以折出一个五边形DMNPQ.
处,得折痕MN、QP.这样,就可以折出一个五边形DMNPQ.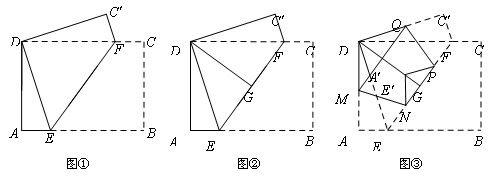
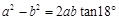 ; ②
; ②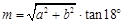 ;
;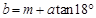 ; ④
; ④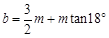 .
.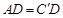 (答案不惟一,也可以是
(答案不惟一,也可以是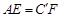 等);(Ⅱ)①②③
等);(Ⅱ)①②③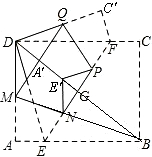
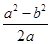 .∵tan∠ADE=tan18°=
.∵tan∠ADE=tan18°=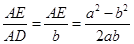 ,∴a2-b2=2abtan18°,即①正确;
,∴a2-b2=2abtan18°,即①正确;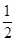 DB=
DB= ,NG=
,NG=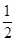 DM=
DM=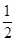 m,NG⊥BD,∴tan∠GBN=tan18°=NG:BG=
m,NG⊥BD,∴tan∠GBN=tan18°=NG:BG=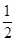 m:
m: .
.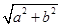 •tan18°,即②正确.
•tan18°,即②正确.

科目:初中数学 来源:不详 题型:解答题
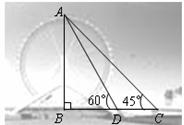
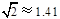 ,
,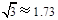 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
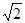 ≈1.41,
≈1.41, ≈1.73,
≈1.73,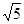 ≈2.24,
≈2.24, ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
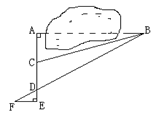
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com