
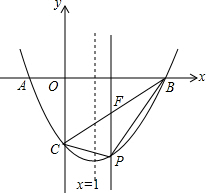
 ��ͼ����ƽ��ֱ������ϵ�У���A��C������ֱ�Ϊ��-1��0������0��-6����B��x���ϣ���֪ij���κ�����ͼ��A��B��C���㣬�����ĶԳ���Ϊֱ��x=1����PΪֱ��BC�·��Ķ��κ���ͼ���ϵ�һ�����㣨��P��B��C���غϣ�������P��y���ƽ���߽�BC�ڵ�F��
��ͼ����ƽ��ֱ������ϵ�У���A��C������ֱ�Ϊ��-1��0������0��-6����B��x���ϣ���֪ij���κ�����ͼ��A��B��C���㣬�����ĶԳ���Ϊֱ��x=1����PΪֱ��BC�·��Ķ��κ���ͼ���ϵ�һ�����㣨��P��B��C���غϣ�������P��y���ƽ���߽�BC�ڵ�F������ ��1���ɶԳ��Կ����B�����꣬���ô���ϵ��������ö��κ����Ľ���ʽ��
��2����B��C�����꣬���ô���ϵ���������ֱ��BC�Ľ���ʽ��
��3������m�ɷֱ��ʾ��P��F�����꣬��ɱ�ʾ��PF�ij�������S��PBC=$\frac{1}{2}$PF•OB������m��ʾ����PBC����������ö��κ��������ʿ���������ֵ����ȡ�����ֵʱ��P�����ꣻ����m�ɷֱ��ʾ��CF��PF�ij�����PC=PF��PC=CF��PF=CF����������ֱ���m��ֵ���ɣ�
��� �⣺
��1����A��-1��0����B����x���ϣ�
��A��B���ڶԳ���x=1�Գƣ�
��B��3��0����
�������߽���ʽΪy=ax2+bx+c��
��A��B��C����������������߽���ʽ�ɵ�$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=-6}\end{array}\right.$�����$\left\{\begin{array}{l}{a=2}\\{b=-4}\\{c=-6}\end{array}\right.$��
�������߽���ʽΪy=2x2-4x-6��
��2����C��0��-6����
�����ֱ��BC����ʽΪy=kx-6��
��B���������ɵ�3k-6=0�����k=2��
��ֱ��BC����ʽΪy=2x-6��
��3�����������֪P��m��2m2-4m-6����F��m��2m-6����
�ߵ�PΪֱ��BC�·��Ķ��κ���ͼ���ϵ�һ�����㣨��P��B��C���غϣ���
��PF=2m-6-��2m2-4m-6��=-2m2+6m��
��S��PBC=$\frac{1}{2}$PF•OB=$\frac{1}{2}$��3��-2m2+6m��=-3��m-$\frac{3}{2}$��2+$\frac{27}{4}$��
��-3��0��
�൱m=$\frac{3}{2}$ʱ��S��PBC�����ֵ�����ֵΪ$\frac{27}{4}$����ʱP������Ϊ��$\frac{3}{2}$��-$\frac{15}{2}$����
�ۡ�P��m��2m2-4m-6����F��m��2m-6����C��0��-6����
��PC=$\sqrt{{m}^{2}+��2{m}^{2}-4m-6+6��^{2}}$=$\sqrt{4{m}^{4}-16{m}^{3}+16{m}^{2}}$=2|m��m-2��|��
PF=-2m2+6m��FC=$\sqrt{{m}^{2}+��2m-6+6��^{2}}$=$\sqrt{5}$|m|��
�ߡ�PCFΪ���������Σ�
����PC=PF��PC=CF��PF=CF���������
��PC=PFʱ������2|m��m-2��|=-2m2+6m�����m=0����C���غϣ���ȥ����m=$\frac{5}{2}$��
��PC=CFʱ������2|m��m-2��|=$\sqrt{5}$|m|�����m=0����ȥ����m=2-$\frac{\sqrt{5}}{2}$��m=2+$\frac{\sqrt{5}}{2}$������3����ȥ����
��PF=CFʱ������-2m2+6m=$\sqrt{5}$|m|�����m=0����ȥ����m=$\frac{6-\sqrt{5}}{2}$��
���Ͽ�֪����PCFΪ����������ʱm��ֵΪ$\frac{5}{2}$��2-$\frac{\sqrt{5}}{2}$��m=$\frac{6-\sqrt{5}}{2}$��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ���������κ��������ʡ������ε���������������ε����ʡ����ɶ���������˼�뼰��������˼���֪ʶ���ڣ�1�������B�������ǽ���Ĺؼ����ڣ�3���٢�����m��ʾ��PF�ij��ǽ���Ĺؼ����ڣ�3��������m��ʾ��PC��PF��CF�ij��ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
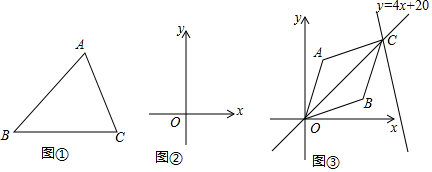
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
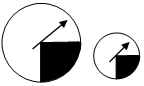 �д�С����ת�̣����к�ɫ���������Ľ�Ϊ90������Σ�Ϊ��̽��ָ�����ں�ɫ�����Ƶ�ʣ��������˷ֱ�ת����ת�̣���¼�±���A��ָ�����ڴ�ת�̵ĺ�ɫ����Ƶ����B����ת���е�Ƶ�ʣ�C��ָ������Сת�̵ĺ�ɫ����Ƶ����D��Сת������ӦƵ�ʣ�
�д�С����ת�̣����к�ɫ���������Ľ�Ϊ90������Σ�Ϊ��̽��ָ�����ں�ɫ�����Ƶ�ʣ��������˷ֱ�ת����ת�̣���¼�±���A��ָ�����ڴ�ת�̵ĺ�ɫ����Ƶ����B����ת���е�Ƶ�ʣ�C��ָ������Сת�̵ĺ�ɫ����Ƶ����D��Сת������ӦƵ�ʣ�| ���� | 25 | 50 | 75 | 100 | 125 | 150 | 175 | 200 | 225 |
| A | 8 | 15 | 21 | 26 | 32 | 36 | 44 | 51 | 57 |
| B | 0.32 | 0.30 | 0.28 | 0.26 | 0.256 | 0.24 | 0.251 | 0.255 | 0.253 |
| C | 8 | 13 | 21 | 26 | 32 | 37 | 43 | 49 | 55 |
| D | 0.32 | 0.26 | 0.28 | 0.26 | 0.256 | 0.247 | 0.246 | 0.245 | 0.244 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com