
【题目】在一条不完整的数轴上从左到右有点![]() ,其中点
,其中点![]() 到点
到点![]() 的距离为3,点
的距离为3,点![]() 到点
到点![]() 的距离为7,如图所示:设点
的距离为7,如图所示:设点![]() 所对应的数的和是
所对应的数的和是![]() .
.
(1)若以![]() 为原点,则
为原点,则![]() 的值是 .
的值是 .
(2)若原点![]() 在图中数轴上,且点
在图中数轴上,且点![]() 到原点
到原点![]() 的距离为4,求
的距离为4,求![]() 的值.
的值.
(3)动点![]() 从
从![]() 点出发,以每秒2个单位长度的速度向终点
点出发,以每秒2个单位长度的速度向终点![]() 移动,动点
移动,动点![]() 同时从
同时从![]() 点出发,以每秒1个单位的速度向终点
点出发,以每秒1个单位的速度向终点![]() 移动,当几秒后,
移动,当几秒后,![]() 两点间的距离为2?(直接写出答案即可)
两点间的距离为2?(直接写出答案即可)
![]()
【答案】(1)-17;(2)m=-5或-29;(3)1秒或5秒.
【解析】
(1)根据已知点A到点B的距离为3和点C到点B的距离为7求出即可;
(2)分为两种情况,当O在C的左边时,当O在C的右边时,求出每种情况A、B、C对应的数,即可求出m;
(3)分为两种情况,当P在Q的左边时,当P在Q的左边时,假如C为原点,求出P、Q对应的数,列出算式,即可求出t.
(1)当以C为原点时,A、B对应的数分别为-10,-7,
则m=-10+(-7)+0=-17,
故答案为:-17;
(2)当O在C的左边时,A、B、C三点在数轴上所对应的数分别为-6、-3、4,
则 m=-6-3+4=-5,
当O在C的右边时,A、B、C三点在数轴上所对应的数分别为-14、-11、-4,
则m=-14-11-4=-29,
综上所述:m=-5或-29;
(3)假如以C为原点,则A、B、C对应的数为-10,-7,0,Q对应的数是-(7-t),P对应的数是-(10-2t),
当P在Q的左边时,[-(7-t)]-[-(10-2t)]=2,
解得:t=1
当P在Q的右边时,[-(10-2t)]-[-(7-t)]=2,
解得:t=5,
即当1秒或5秒后,P、Q两点间的距离为2.


科目:初中数学 来源: 题型:
【题目】为了了解2019年北京市乘坐地铁的每个人的月均花费情况,相关部门随机调查了1000人乘坐地铁的月均花费(单位:元),绘制了如下频数分布直方图,根据图中信息,下面三个推断中,合理的是( )
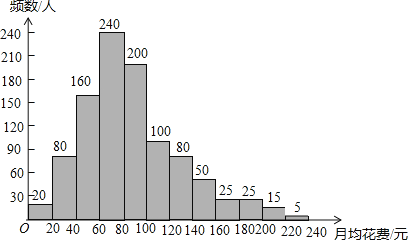
①小明乘坐地铁的月均花费是75元,那么在所调查的1000人中一定有超过一半的人月均花费超过小明;
②估计平均每人乘坐地铁的月均花费的不低于60元;
③如果规定消费达到一定数额可以享受折扣优惠,并且享受折扣优惠的人数控制在20%左右,那么乘坐地铁的月均花费达到120元的人可享受折扣.
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
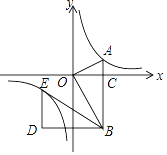
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
(1)求k的值;
(2)若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某种产品展开图,高为3cm.
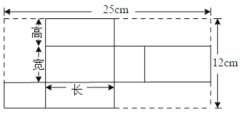
(1)求这个产品的体积.
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
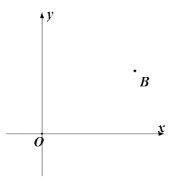
【题目】如图,在平面直角坐标系第一象限中有一点B. 要求:用尺规作图作一条直线AC,使它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC全等.
(1)小明的作法是:过B点分别向x 轴、y 轴作垂线,垂足为A、C,连接A、C,则直线AC即为所求.请你帮助小明在图中完成作图(保留作图痕迹);
图
(2)请在图中再画出另一条满足条件的直线AC,并说明理由.
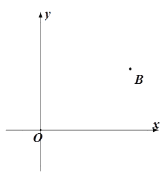
图
查看答案和解析>>
科目:初中数学 来源: 题型:
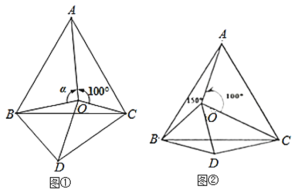
【题目】如图①,点![]() 是等边
是等边![]() 内一点,
内一点,![]() ,
,![]() .以
.以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 时(如图②),试判断
时(如图②),试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)求当![]() 是多少度时,
是多少度时,![]() 是等腰三角形?(写出过程)
是等腰三角形?(写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式,然后由(x+m)2≥0就可求出多项式x2+bx+c的最小值.
例题:求x2-12x+37的最小值.
解:x2-12x+37=x2-2x·6+62-62+37=(x-6)2+1,
因为不论x取何值,(x-6)2总是非负数,即(x-6)2≥0,
所以(x-6)2+1≥1.
所以当x=6时,x2-12x+37有最小值,最小值是1.
根据上述材料,解答下列问题:
(1)填空:x2-8x+_________=(x-_______)2,
(2)将x2+10x-2变形为(x+m)2+n的形式,并求出x2+10x-2的最小值,
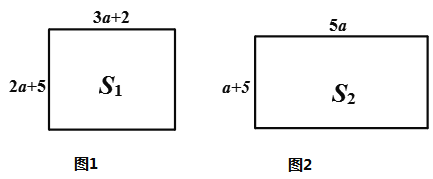
(3)如图①所示的长方形边长分别是2a+5、3a+2,面积为S1:如图②所示的长方形边长分别是5a、a+5,面积为S2. 试比较S1与S2的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=10cm,AM=3cm,求CN的长;
(2)如果MN=6cm,求AB的长.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com