
【题目】如图1.△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC作等腰Rt△ABE和等腰Rt△ACF,过点E,F作射线GA的垂线,垂足分别为P,Q.
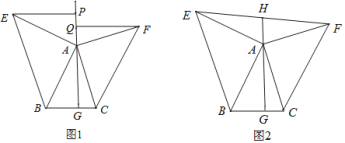
(1)求证:△EPA≌△AGB:
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
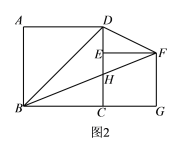
(3)如图2.若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由:
(4)在(3)的条件下,若BC=10,AG=12.请直接写出S△AEF= .
【答案】(1)证明见解析;(2)结论:EP=FQ,证明见解析;(3)结论:EH=FH,理由见解析;(4)60.
【解析】
(1)根据等腰Rt△ABE的性质,求出∠EPA=∠EAB=∠AGB=90°,∠PEA=∠BAG,根据AAS推出△EPA≌△AGB.
(2)根据全等三角形的性质推出EP=AG,同理可得△FQA≌△AGC,即可得出AG=FQ,最后等量代换即可得出答案.
(3)求出∠EPH=∠FQH=90°,根据AAS推出△EPH≌△FQH,即可得出EH与FH的大小关系.
(4)根据全等三角形△EPH≌△FQH,△EPA≌△AGB,△FQA≌△AGC,推出S△FQA=S△AGC,S△FQH=S△EPH,S△EPA=S△AGB,即可求出S△AEF=S△ABC,根据三角形面积公式求出即可.
解:(1)如图1,∵∠EAB=90°,EP⊥AG,AG⊥BC,
∴∠EPA=∠EAB=∠AGB=90°,
∴∠PEA+∠EAP=90°,∠EAP+∠BAG=90°,
∴∠PEA=∠BAG,
在△EPA和△AGB中,

∴△EPA≌△AGB(AAS),
(2)结论:EP=FQ,
证明:由(1)可得,△EPA≌△AGB,
∴EP=AG,
如图1,∵∠FAC=90°,FQ⊥AG,AG⊥BC,
∴∠FQA=∠FAC=∠CGA=90°,
∴∠FAQ+∠AFQ=90°,∠FAQ+∠GAC=90°,
∴∠AFQ=∠GAC,
在△QFA和△GAC中,
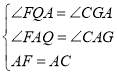
∴△QFA≌△GAC(AAS),
∴AG=FQ,
∴EP=FQ;
(3)结论:EH=FH,
理由:如图,∵EP⊥AG,FQ⊥AG,
∴∠EPH=∠FQH=90°,
在△EPH和△FQH中,

∴△EPH≌△FQH(AAS),
∴EH=FH.
(4))∵△EPH≌△FQH,△EPA≌△AGB,△FQA≌△AGC,
∴S△FQA=S△AGC,S△FQH=S△EPH,S△EPA=S△AGB,
∴S△AEF=S△EPA+S△FQA
=S△AGB+S△AGC
=S△ABC
=![]() ×BC×AG
×BC×AG
=![]() ×10×12
×10×12
=60
故答案为:60.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.
(1)设该学校所买的电脑台数是x台,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别写出
元,请分别写出![]() ,
, ![]() 与x之间的关系式;
与x之间的关系式;
(2)该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).

请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中,D类二手轿车交易辆数所对应扇形的圆心角为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C 重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD.
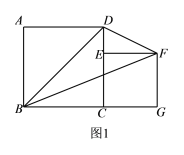
(1)当点E与点D重合时,△BDF的面积为 ;当点E为CD的中点时,△BDF的面积为 .
(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想;
(3)如图2,设BF与CD相交于点H,若△DFH的面积为![]() ,求正方形CEFG的边长.
,求正方形CEFG的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=![]() ,则称点Q为点P的“亲密点”.即:当x≥0时,点P(x,y)的“亲密点”Q的坐标为(x,y+1);当x<0时,点P(x,y)的“亲密点”Q的坐标为(x,-y).例如:点(1,2)的“亲密点”为点(1,3),点(-1,3)的“亲密点”为点(-1,-3).
,则称点Q为点P的“亲密点”.即:当x≥0时,点P(x,y)的“亲密点”Q的坐标为(x,y+1);当x<0时,点P(x,y)的“亲密点”Q的坐标为(x,-y).例如:点(1,2)的“亲密点”为点(1,3),点(-1,3)的“亲密点”为点(-1,-3).
(1)点(2,-3)的“亲密点”为______;______的“亲密点”是(-2,-5).
(2)点M(m+1,5)是一次函数y=x+3图象上点N的“亲密点”,求点N的坐标.
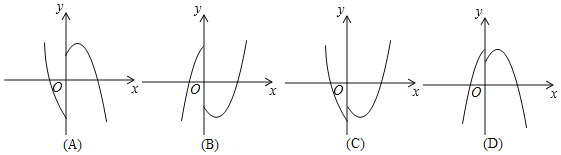
(3)若点P在函数y=x2-2x-3的图象上.则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是______.
(4)若点P在二次函数y=x2-2x-5的图象上,当-2<x≤a时,其亲密点Q的纵坐标y′满足-5≤y′≤5,请直接写出a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com