
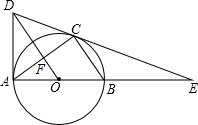
 如图,AB为⊙O的直径,点C在⊙O上,连接BC、AC,作OD∥BC,与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,AB为⊙O的直径,点C在⊙O上,连接BC、AC,作OD∥BC,与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.分析 (1)根据全等三角形的判定得出△COD≌△AOD,推出∠DCO=∠DAO=90°,根据切线的判定得出即可;
(2)设BC=a,则AB=$\sqrt{3}$a,求出AC=$\sqrt{2}$a,证△EBC∽△ECA,根据相似三角形的性质得出$\frac{EB}{EC}$=$\frac{BC}{AC}$=$\frac{1}{\sqrt{2}}$,求出EC=6$\sqrt{2}$,求出DA=DC=$\sqrt{2}$OB=$\frac{\sqrt{6}}{2}$a,
在Rt△DAE中,由勾股定理得出方程,求出a的值,即可得出答案.
解答 (1)证明:连接OC,
∵OD∥BC,
∴∠OBC=∠DOA,∠DOC=∠BCO,
∵BO=OC,
∴∠OBC=∠BCO,
∴∠AOD=∠COD,
在△COD和△AOD中,
$\left\{\begin{array}{l}{OC=OA}\\{∠COD=∠AOD}\\{OD=OD}\end{array}\right.$,
∴△COD≌△AOD(SAS),
∴∠DCO=∠DAO,
∵AD是⊙O的切线,
∵∠DAO=90°,
∴∠DCO=90°,
即OC⊥DE,
∵OC为半径,
∴DE是⊙O的切线;
(2)设BC=a,则AB=$\sqrt{3}$a,
所以AC=$\sqrt{2}$a,
∵DE为⊙O的切线,
∴∠BCE=∠CAE,
∵∠E=∠E,
∴△EBC∽△ECA,
∴$\frac{EB}{EC}$=$\frac{BC}{AC}$=$\frac{1}{\sqrt{2}}$,
∴EC=6$\sqrt{2}$,
又∵OD∥BC,
∴$\frac{OB}{CD}$=$\frac{EB}{EC}$=$\frac{1}{\sqrt{2}}$,
∴DA=DC=$\sqrt{2}$OB=$\frac{\sqrt{6}}{2}$a,
在Rt△DAE中,由勾股定理得:($\frac{\sqrt{6}}{2}$a)2+($\sqrt{3}$a+6)2=($\frac{\sqrt{6}}{2}$a+6$\sqrt{2}$)2,
解得:a=2$\sqrt{3}$,
∴AD=$\frac{\sqrt{6}}{2}$a=3$\sqrt{2}$.
点评 本题考查了相似三角形的性质和判定,勾股定理,切线的性质和判定的应用,能综合运用性质进行推理是解此题的关键,综合性比较强,难度偏大.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:选择题
 如图,点A是过点(1,4)的双曲线y=$\frac{k}{x}$上第一象限内的任意一点,AB⊥x轴,垂足为B,点C是x轴上点B右侧的任意一点,点D是线段AC的中点,直线BD交y轴于点E,则△BCE的面积为( )
如图,点A是过点(1,4)的双曲线y=$\frac{k}{x}$上第一象限内的任意一点,AB⊥x轴,垂足为B,点C是x轴上点B右侧的任意一点,点D是线段AC的中点,直线BD交y轴于点E,则△BCE的面积为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+2)2+4 | B. | y=(x-4)2+4 | C. | y=(x+2)2 | D. | y=(x-4)2+6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,等边△BCD中,BC=2$\sqrt{3}$,过C作CA⊥BC,且AC=2,连接AB交CD于点F,将△ABC绕点B顺时针旋转,使得点C与点D重合,得到△EBD,连接FE,则EF的长为( )
如图,等边△BCD中,BC=2$\sqrt{3}$,过C作CA⊥BC,且AC=2,连接AB交CD于点F,将△ABC绕点B顺时针旋转,使得点C与点D重合,得到△EBD,连接FE,则EF的长为( )| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\frac{6\sqrt{13}}{7}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
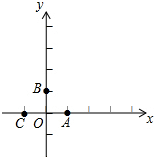 如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P7的坐标是(2,0),点P2016的坐标为(0,0).
如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P7的坐标是(2,0),点P2016的坐标为(0,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 27~30 | 21 | 0.35 |
| B | 23~26 | m | x |
| C | 19~22 | n | y |
| D | 18及18以下 | 3 | 0.05 |
| 合计 | 60 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲地气温 | 24 | 30 | 28 | 24 | 22 | 26 | 27 | 26 | 29 | 24 |
| 乙地气温 | 24 | 26 | 25 | 26 | 24 | 27 | 28 | 26 | 28 | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com