
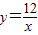 ,是否存在点P,使得四边形ABCD面积取得最值?若存在,求出点P的坐标;若不存在,请说明理由.
,是否存在点P,使得四边形ABCD面积取得最值?若存在,求出点P的坐标;若不存在,请说明理由.
 AC•BD得出有关m的二次函数解析式,进而求出最值即可;
AC•BD得出有关m的二次函数解析式,进而求出最值即可; AC•BD利用完全平方公式性质,进而得出四边形ABCD面积取最小值.
AC•BD利用完全平方公式性质,进而得出四边形ABCD面积取最小值. AC•BD=
AC•BD= (m+3)(n+4)=
(m+3)(n+4)= (mn+12+4m+3n)
(mn+12+4m+3n) (m-3)2+18,
(m-3)2+18, AC•BD=
AC•BD= (m+3)(n+4)=
(m+3)(n+4)= (mn+12+4m+3n),
(mn+12+4m+3n), ),
),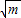 -
- )2+24,
)2+24,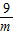 (m>0),即m=3时,四边形ABCD面积取最小值为24,
(m>0),即m=3时,四边形ABCD面积取最小值为24,

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
| 3 |
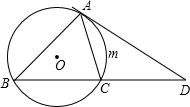 =2,∠ADC=30°
=2,∠ADC=30°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com