
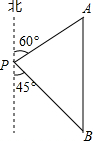
 某学生参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离.
某学生参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离.科目:初中数学 来源:2013届北京市怀柔区九年级上学期期末考试数学试卷(带解析) 题型:解答题
某学生参加社会实践活动,在景点P处测得景点B位于南偏东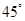 方向,然后沿北偏东
方向,然后沿北偏东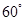 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之的距离.
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之的距离.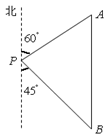
查看答案和解析>>
科目:初中数学 来源:2013届山西省农业大学附属中学九年级下学期中考练兵数学试卷(带解析) 题型:解答题
某学生参加社会实践活动,在景点P处测得景点B位于南偏东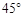 方向,然后沿北偏东
方向,然后沿北偏东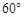 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年山西省九年级下学期中考练兵数学试卷(解析版) 题型:解答题
某学生参加社会实践活动,在景点P处测得景点B位于南偏东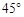 方向,然后沿北偏东
方向,然后沿北偏东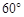 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。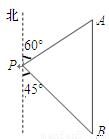
查看答案和解析>>
科目:初中数学 来源:2012-2013学年北京市怀柔区九年级上学期期末考试数学试卷(解析版) 题型:解答题
某学生参加社会实践活动,在景点P处测得景点B位于南偏东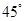 方向,然后沿北偏东
方向,然后沿北偏东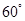 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之的距离.
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之的距离.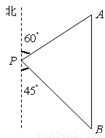
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com