
����Ŀ����֪������y��ax2��2ax+3��x�ύ�ڵ�A��B��A��B�ң�����AB��4����y�ύ��C�㣮
��1���������ߵĽ���ʽ��
��2����ͼ��֤�����������������һ��P��0��b����b��3�������ڹ���P��һ��ֱ�߽���������M��N���㣬ʹ��PM��MN������
��3��������������0��x��4��IJ��ּ�Ϊͼ��G����ͼ��G��ֱ��y��t�Ϸ��IJ�����y��t���ۣ����ಿ�ֱ��ֲ��䣬�õ�һ���µĺ�����ͼ��������������ֵΪm����СֵΪn����m��n��6����t��ȡֵ��Χ��

���𰸡���1��y����x2+2x+3����2�������������3����2��t��1��
��������
��1��������y��ax2��2ax+3�ĶԳ���Ϊx��1����AB��4���ɶԳ��Ե�A����1��0����B��3��0����������⣻
��2��֤����PMG�ա�NMH��AAS����yG+yH��2yM��������⣻
��3���ֵ�D���ڵ�H��4��-5���Ϸ�����D���ڵ�H��4��-5���·�����������ֱ���⼴�ɣ�
�⣺��1��������y��ax2��2ax+3�ĶԳ���Ϊx��1����AB��4���ɶԳ��Ե�A��-1��0����B��3��0����

��A��-1��0������y��ax2��2ax+3����a+2a+3��0����a��-1��
�������ߵĽ���ʽΪy��-x2+2x+3��
��2����ͼ����M��GH��x�ᣬPG��x�ᣬNH��x�ᣬ
��PM��MN�����PMG�ա�NMH��AAS����
��PG��NH��MG��MH��
��M��m��-m2+2m+3������N��2m��-4m2+4m+3����
��P��0��b����GM��MH��
��yG+yH��2yM��
��b+��-4m2+4m+3����2��-m2+2m+3������2m2��b-3��
��b��3��
�����m�ķ���������������ȵ�ʵ������
�˼�˵���˵�M��N���ڣ���ʹ��PM��MN��֤�ϣ�
��3��ͼ����ǰ������ͼ��ʾ���䶥��ֱ�ΪD��1��4����D����1��2t��4����

�ٵ�D���ڵ�H��4��-5���Ϸ�ʱ��
2t��4��-5����t��-![]() ��
��
��ʱ��m��t��n��-5����m-n��6����t+5��6����t��1��
��-![]() ��t��1��
��t��1��
�ڵ���D���ڵ�H��4��-5���·�ʱ��
ͬ���ɵã�t��-![]() ��m��t��n��2t-4��
��m��t��n��2t-4��
��m-n��6����t-��2t-4����6��
��t��-2����-2��t��-![]() ��
��
����������t��ȡֵ��ΧΪ����2��t��1��


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʡij����Ϊȫ�˻������һ��ɱ�ÿ��20Ԫ�Ĺ���Ʒ��Ͷ���г���������������y���������ۼ�x(Ԫ/��)��һ�κ��������ۼ�Ϊ23Ԫ/��ʱ��ÿ��������Ϊ790�������ۼ�Ϊ25Ԫ/����ÿ��������Ϊ750��.
��1����y��x�ĺ�����ϵ��
��2������ù���Ʒ��߲�����ÿ��30Ԫ����ô�ۼ۶�λÿ������Ԫʱ�����ճ����۸ù���Ʒÿ���õ����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �IJ���ͼ���䶥��Ϊ
�IJ���ͼ���䶥��Ϊ![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ���һ������Ϊ
���һ������Ϊ![]() ������
������![]() .���½��ۣ���
.���½��ۣ���![]() ���������߾�����
���������߾�����![]() ����
����![]() ���ܵ�
���ܵ�![]() ʱ��
ʱ�� ![]() .������ȷ���ǣ� ��
.������ȷ���ǣ� ��

A.�٢�B.�ڢ�C.�٢�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��4��23�գ�Ϊӭ�����������������ij��ǿ�չ�����н��.�˿�ÿ������100Ԫ���һ���������ᣬ����Ϊ��һ�������Ĵ�����װ��4��С��С���Ϸֱ��������1��2��3��4�����dz�������������ȫ��ͬ��ҡ�Ⱥ�ͬʱ���������������С����������������֮���뽱���Ĺ���ȯ���Ķ�Ӧ��ϵ���£�
������������֮�� | 3 | 4 | 5 | 6 | 7 |
�����Ĺ���ȯ��Ԫ�� | 0 | 0 | 30 | 60 | 90 |
��1��ͨ���б�����״ͼ�ķ�����������һ�λ��90Ԫ����ȯ�ĸ��ʣ�
��2����ǹ涨������˿Ͳ�Ը��μ���������ô����ֱ�ӻ��30Ԫ�Ĺ���ȯ.�����μ�����������ֱ�ӻ�ù���ȯ�����ַ�ʽ�У�����Ϊ���ַ�ʽ�Թ˿����㣿��ͨ����ƽ���̵ķ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB��4��E��F�ֱ��DZ�AB��AD�ϵĶ��㣬AE��DF������DE��CF���ڵ�P������P��PK��BC����PK��2������CBK�Ķ������ʱ����BK��Ϊ_____��
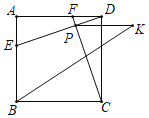
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ���̵���5Ԫ/ǧ�˵ļ۸�һ��ˮ���������ۣ����������������5%�����������0.7Ԫ/ǧ�ˣ����費����������
��1���̵�Ҫ��ˮ���������ٶ���Ϊ����Ԫ�Ų��������
��2�������۹����У��̵귢��ÿ����֦��������m��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�֮�������ϵm����10x+120����ô�����۵��۶�Ϊ����ʱ��ÿ���õ�����w���
��3�����̵����ÿ����һǧ��ˮ���;���aԪ����a��1����ϣ�����̣�ͨ�����ۼ�¼���֣�����۸����ÿǧ��11Ԫʱ���۳�������ÿ���������x�������С��ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��O�Ǿ���ABCD�ĶԽ��ߵĽ��㣬E��F��G��H�ֱ���OA��OB��OC��OD�ϵĵ㣬��AE��BF��CG��DH.
(1)��֤���ı���EFGH�Ǿ��Σ�
(2)��E��F��G��H�ֱ���OA��OB��OC��OD���е㣬��DG��AC��OF��2cm�������ABCD�������
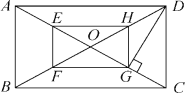
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ�AB��6��BC��4����E�ڱ�AB�ϣ������A��B�غϣ�������D��DF��DE������BC���ӳ����ڵ�F��

��1����֤����DAE�ס�DCF��
��2�����߶�AE�ij�Ϊx���߶�BF�ij�Ϊy����y��x֮��ĺ�����ϵʽ��
��3�����ı���EBFDΪ��Գ�ͼ��ʱ����cos��AED��ֵΪ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2��bx��c�������ϣ���x�ύ�ڵ�A��B����y�ύ�ڵ�C
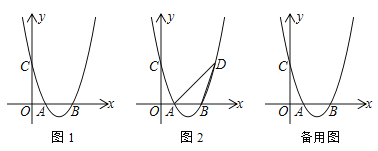
(1) ��ͼ1����A (1��0)��C (0��3)�ҶԳ���Ϊֱ��x��2���������ߵĽ���ʽ
(2) ��(1)�������£���ͼ2������C���������߶Գ���ĶԳƵ�D������AD��BD�������������Ƿ���ڵ�P��ʹ��PAD����ADB�������ڣ������P�����꣬�������ڣ���˵������
(3) ��ֱ��l��y��mx��n������������������M��N��M��N����ߣ���QΪ��������һ�㣨����M��N�غϣ�������Q��QHƽ����y�ύֱ��l�ڵ�H����![]() ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com