练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

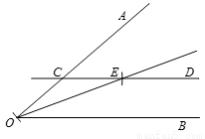
    小米是一个爱动脑筋的孩子，他用如下方法作∠AOB的角平分线：作法：如图，

    （1）在射线OA上任取一点C，过点C作CD∥OB；

    （2）以点C为圆心，CO的长为半径作弧，交CD于点E；

    （3）作射线OE．

    所以射线OE就是∠AOB的角平分线．

    请回答：小米的作图依据是_______________________

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届辽宁省盘锦市九年级下学期第二次模拟考试数学试卷（解析版） 题型：单选题

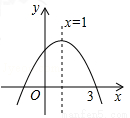
    二次函数的图象如图所示，有下列结论：①；

    ②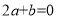；③；④若且，则；⑤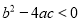．其中正确的有（　　　）

    A. ①②⑤ B. ②③⑤ C. ③④ D. ②④

    查看答案和解析>>

    科目：初中数学 来源：2017届湖北省武汉市中考模拟数学试卷（一）（解析版） 题型：填空题

    如图，△ABC内接于⊙O，BC＝12，∠A＝60°，点D为弧BC上一动点，BE⊥直线OD于点E．当点D从点B沿弧BC运动到点C时，点E经过的路径长为___________

    查看答案和解析>>

    科目：初中数学 来源：2017届北京市平谷区4月初三统一练习（一）数学试卷（解析版） 题型：解答题

    在△ABC中，AB=AC，∠A=60°，点D是BC边的中点，作射线DE，与边AB交于点E，射线DE绕点D顺时针旋转120°，与直线AC交于点F．

    （1）依题意将图1补全；

    （2）小华通过观察、实验提出猜想：在点E运动的过程中，始终有DE=DF．小华把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

    想法1：由点D是BC边的中点，通过构造一边的平行线，利用全等三角形，可证DE=DF；

    想法2：利用等边三角形的对称性，作点E关于线段AD的对称点P，由∠BAC与∠EDF互补，可得∠AED与∠AFD互补，由等角对等边，可证DE=DF；

    想法3：由等腰三角形三线合一，可得AD是∠BAC的角平分线，由角平分线定理，构造点D到AB，AC的高，利用全等三角形，可证DE=DF…….

    请你参考上面的想法，帮助小华证明DE=DF（选一种方法即可）；

    （3）在点E运动的过程中，直接写出BE，CF，AB之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源：2017届北京市平谷区4月初三统一练习（一）数学试卷（解析版） 题型：解答题

    在平面直角坐标xOy中，直线与双曲线的一个交点为A（﹣2，3），与x轴交于点B．

    (1) 求m的值和点B的坐标；

    (2) 点P在y轴上，点P到直线的距离为，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源：2017届北京市平谷区4月初三统一练习（一）数学试卷（解析版） 题型：填空题

    如果分式的值为0，那么x的值是__________．

    查看答案和解析>>

    科目：初中数学 来源：2017届北京市平谷区4月初三统一练习（一）数学试卷（解析版） 题型：单选题

    如果x+y=4，那么代数式的值是（ ）

    A. ﹣2 B. 2 C. D.

    查看答案和解析>>

    科目：初中数学 来源：2017届广东省广州市番禺区九年级中考一模数学试卷（解析版） 题型：填空题

    方程组的解是____．

    查看答案和解析>>

    科目：初中数学 来源：2017届湖南省张家界市永定区九年级下学期期中考试（一模）数学试卷（解析版） 题型：解答题

    如图，在平行四边形ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．求证：△ABE≌△CDF.

    查看答案和解析>>

    同步练习册答案