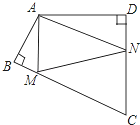
【题目】如图，AB⊥BC，AD⊥DC，∠BAD=110°，在BC、CD上分别找一点M、N，当△AMN周长最小时，∠MAN的度数为 度．
【答案】40
【解析】
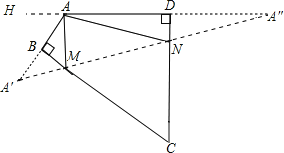
试题分析：根据要使△AMN的周长最小，即利用点的对称，使三角形的三边在同一直线上，作出A关于BC和CD的对称点A′，A″，即可得出∠AA′M+∠A″=∠HAA′=70°，进而得出∠MAB+∠NAD=70°，即可得出答案．
解：作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值，作DA延长线AH，．
∵∠DAB=110°，
∴∠HAA′=70°，
∴∠AA′M+∠A″=∠HAA′=70°，
∵∠MA′A=∠MAB，∠NAD=∠A″，
∴∠MAB+∠NAD=70°，
∴∠MAN=110°﹣70°=40°，
故答案为：40．
科目：初中数学 来源： 题型：
【题目】在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是（ ）
A. AC＝BD，AB∥CD，AB＝CDB. AD∥BC，∠A＝∠C
C. AO＝BO＝CO＝DO，AC⊥BDD. AO＝CO，BO＝DO，AB＝BC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】据2010年第六次全国人口普查公布的数据显示，全桂林市总人口为498.84万人，那么用科学记数法表示为（ ）人．
A. 4.98846 B. 4.9884×106 C. 4.9884×107 D. 4.9884×108
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A(0，－1)，M(1，2)，N(－3，0)，则射线AM和射线AN组成的角的度数（ ）
A. 一定大于90° B. 一定小于90°
C. 一定等于90° D. 以上三种情况都有可能
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们把a、b中较小的数记作min{a，b}，设函数f (x)={
，|x－2|}．若动直线y=m与函数y=f (x)的图象有三个交点，它们的横坐标分别为x1、x2、x3，则x1x2x3的最大值为_________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明和小丽是同班同学，小明的家距学校2千米远，小丽的家距学校5千米远，设小明家距小丽家x千米远，则x的值应满足（ ）
A．x=3 B．x=7 C．x=3或x=7 D．3≤x≤7
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC．
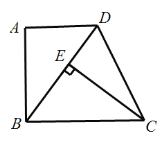
（1）求证：△ABD≌△ECB；
（2）若∠EDC=65°，求∠ECB的度数；
（3）若AD=3，AB=4，求DC的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com