
【题目】如图,AD 是△ABC 的角平分线,DE,DF 分别是△BAD 和△ACD 的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形 AEDF 是正方形;④AE+DF=AF+DE.其中正确的是_________(填序号).

【答案】②③④.
【解析】
①如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,所以①不正确;
②首先根据全等三角形的判定方法,判断出△AED≌△AFD,AE=AF,DE=DF;然后根据全等三角形的判定方法,判断出△AE0≌△AFO,即可判断出AD⊥EF;
③首先判断出当∠A=90°时,四边形AEDF的四个角都是直角,四边形AEDF是矩形,然后根据DE=DF,判断出四边形AEDF是正方形即可;
④根据△AED≌△AFD,判断出AE=AF,DE=DF,即可判断出AE+DF=AF+DE成立.
如果OA=OD,则四边形AEDF是矩形,没有说∠A=90°,不符合题意,故①错误;
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
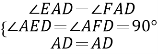
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE+DF=AF+DE,故④正确;
∵在△AEO和△AFO中,
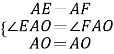 ,
,
∴△AEO≌△AFO(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,故②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,故③正确.
综上可得:正确的是:②③④,
故答案为:②③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
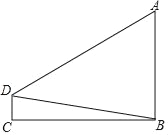
【题目】如图,两座建筑物的水平距离BC为40m,从D点测得A点的仰角为30°,B点的俯角为10°,求建筑物AB的高度(结果保留小数点后一位).
参考数据sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,![]() 取1.732.
取1.732.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
![]() 从今年年初至
从今年年初至![]() 月
月![]() 日,猪肉价格不断走高,
日,猪肉价格不断走高,![]() 月
月![]() 日比年初价格上涨了
日比年初价格上涨了![]() .某市民在今年
.某市民在今年![]() 月
月![]() 日购买
日购买![]() 千克猪肉至少要花
千克猪肉至少要花![]() 元钱,那么今年年初猪肉的最低价格为每千克多少元?
元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)![]() 月
月![]() 日,猪肉价格为每千克
日,猪肉价格为每千克![]() 元
元![]() 月
月![]() 日,某市决定投入储备猪肉并规定其销售价在每千克
日,某市决定投入储备猪肉并规定其销售价在每千克![]() 元的基础上下调
元的基础上下调![]() 出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克
出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克![]() 元的情况下,该天的两种猪肉总销量比
元的情况下,该天的两种猪肉总销量比![]() 月
月![]() 日增加了
日增加了![]() ,且储备猪肉的销量占总销量的
,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比
,两种猪肉销售的总金额比![]() 月
月![]() 日提高了
日提高了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
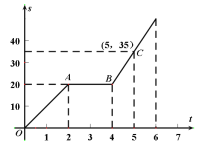
【题目】小明骑自行车从甲地到乙地,图中的折线表示小明行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数关系.试根据函数图像解答下列问题:
之间的函数关系.试根据函数图像解答下列问题:
(1)小明在途中停留了____![]() ,小明在停留之前的速度为____
,小明在停留之前的速度为____![]() ;
;
(2)求线段![]() 的函数表达式;
的函数表达式;
(3)小明出发1小时后,小华也从甲地沿相同路径匀速向乙地骑行,![]()
![]() 时,两人同时到达乙地,求
时,两人同时到达乙地,求![]() 为何值时,两人在途中相遇.
为何值时,两人在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列四个结论,其中正确的结论为( )
A. 等边三角形既是轴对称图形,又是中心对称图形
B. 对角线相等的四边形是矩形
C. 三角形的外心到三个顶点的距离相等
D. 任意三个点都可确定一个圆
查看答案和解析>>
科目:初中数学 来源: 题型:
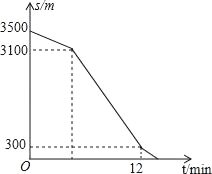
【题目】小刚家、公交车站、学校在一条笔直的公路旁(小刚家、学校到这条公路的距离忽略不计).一天,小刚从家出发去上学,沿这条公路步行到公交站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小刚下车时发现还有4分钟上课,于是他沿着这条公路跑步赶到学校(上、下车时间忽略不计),小刚与学校的距离s(单位:米)与他所用的时间t(单位:分钟)之间的函数关系如图所示.已知小刚从家出发7分钟时与家的距离是1200米,从上公交车到他到达学校共用10分钟.下列说法:
①公交车的速度为400米/分钟;
②小刚从家出发5分钟时乘上公交车;
③小刚下公交车后跑向学校的速度是100米/分钟;
④小刚上课迟到了1分钟.
其中正确的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 经过正方形
经过正方形![]() 的顶点
的顶点![]() ,先分别过此正方形的顶点
,先分别过此正方形的顶点![]() 、
、![]() 作
作![]() 于点
于点![]() 、
、![]() 于点
于点![]() .然后再以正方形对角线的交点
.然后再以正方形对角线的交点![]() 为端点,引两条相互垂直的射线分别与
为端点,引两条相互垂直的射线分别与![]() ,
,![]() 交于
交于![]() ,
,![]() 两点.若
两点.若![]() ,
,![]() ,则线段
,则线段![]() 长度的最小值是___.
长度的最小值是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润![]() (元)与销量
(元)与销量![]() (万辆)的关系如图所示;在国外市场每辆的利润
(万辆)的关系如图所示;在国外市场每辆的利润![]() (元)与销量
(元)与销量![]() (万量)的关系为:
(万量)的关系为:![]() .
.
![]() 求国内市场的销售总利润
求国内市场的销售总利润![]() (万元)关于销售量
(万元)关于销售量![]() (万辆)的函数关系式,并指出自变量的取值范围.
(万辆)的函数关系式,并指出自变量的取值范围.
![]() 该公司的年生产能力为
该公司的年生产能力为![]() 万辆,请帮助该公司确定国内、国外市场的销量各为多少时,公司的年利润最大?
万辆,请帮助该公司确定国内、国外市场的销量各为多少时,公司的年利润最大?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com