练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
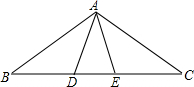
    6．如图，△ABC中，AB=AC，点D、E在BC上，如果只添加一个条件，使得∠DAB=∠EAC，则添加的条件不能为（　　）
    A．∠B=∠CB．BD=CEC．AD=AED．BE=CD

    分析 本题根据添加的条件能证明全等的，就可以添加，否则不能，选项A添加后不能证明两三角形全等，其他三个选项都可以证明全等，由此得出结论．

    解答 解：A、因为AB=AC，可以得出∠B=∠C，如果只添加∠B=∠C，不能得△ABD和△ACE全等，也就不能得出∠DAB=∠EAC；
    B、若添加BD=CE，△ABD和△ACE满足SAS，可以证明全等，从而得出∠DAB=∠EAC；
    C、若添加AD=AE，则∠ADE=∠AED，所以∠ADB=∠AEC，根据AAS可以证明全等，从而得出∠DAB=∠EAC；
    D、若添加BE=CD，则得BD=EC，与选项B相同，可以得到∠DAB=∠EAC；
    所以本题添加的条件不能为A；
    故选A．

    点评 本题主要考查出三角形全等的判定和性质，熟练掌握三角形的判定方法是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．解方程：$\frac{2}{3}$x-（2$\frac{1}{4}$+3.75）=$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

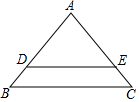    17．如图，点D，E分别是AB和AC上的点，△ADE∽△ABC，AD=2acm，DB=acm，BC=bcm，∠A=70°，∠B=50°．
    （1）求∠ADE的度数；
    （2）求∠AED的度数；
    （3）求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知，在△ABC中，∠BAC=90°，AB=AC，CE平分∠ACB交AB于点E．
    （1）如图1，若点D在斜边BC上，DM垂直平分BE，垂足为M．求证：BD=AE；
    （2）如图2，过点B作BF⊥CE，交CE的延长线与点F．若CE=6，求△BEC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．点A为线段BC外一动点，且BC=3，AB=1．如图所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．
    （1）请找出图中与BE相等的线段，并说明理由；
    （2）直接写出线段BE长的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图1，等腰△ABC中，AB=AC，当顶角∠A的大小确定时，它的对边BC与邻边AB（或AC）的比值也就确定，我们把这个比值记作T（A），即T（A）=$\frac{∠A的对边}{∠A的邻边}$=$\frac{BC}{AB}$，当∠A=60°时，有T（60°）=1．
    （1）理解巩固：T（90°）=$\sqrt{2}$，T（120°）=$\sqrt{3}$，T（A）的值的范围是0＜T（α）＜2；
    （2）学以致用：如图2，圆锥的母线长为9，底面圆的直径PQ=8，一只蚂蚁从点P沿着圆锥的侧面爬行到点Q，求蚂蚁爬行的最短路径长（精确到0.1）．（参考数据：T（160°）≈1.97，T（80°）≈1.29，T（40°）≈0.68）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列结论正确的是（　　）
    A．任何数都不等于它的相反数
    B．符号相反的数互为相反数
    C．若有理数a，b互为相反数，则它们一定异号
    D．若有理数a，b互为相反数，那么a+b=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：
    （1）（xy-x2）÷$\frac{x-y}{xy}$
    （2）（$\frac{a}{a-b}$-$\frac{a}{a+b}$）÷$\frac{2b}{{a}^{2}-{b}^{2}}$
    （3）1÷（2a+$\frac{1-{a}^{2}}{a}$）
    （4）（$\frac{1}{a}$-$\frac{1}{b}$）2÷（$\frac{1}{{a}^{2}}$-$\frac{1}{{b}^{2}}$）
    （5）1-$\frac{x-y}{x+2y}$÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}+4xy+4{y}^{2}}$
    （6）$\frac{m-3}{m}$•$\frac{m}{m+3}$+$\frac{6}{{m}^{2}-9}$÷$\frac{2}{m-3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列各式正确的是（　　）
    A．-（-3）=-|-3|B．-（2）3=-2×3C．|-$\frac{1}{100}$|＞-100D．-24=（-2）4

    查看答案和解析>>

    同步练习册答案