
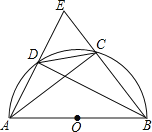
【题目】如图,![]() 是半圆的直径,
是半圆的直径,![]() 的平分线交半圆于
的平分线交半圆于![]() 和
和![]() 的延长线交于圆外一点
的延长线交于圆外一点![]() ,连接
,连接![]() .
.
(1)求证:![]() 是等腰三角形.
是等腰三角形.
(2)若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)8.
【解析】
(1)根据圆周角定理由AB是半圆的直径得∠ADB=∠ACB=90°,加上∠ABC的平分线交半圆于D,根据等腰三角形的判定得BA=BE,再根据等腰三角形的性质得AD=ED,即可得到CD为直角三角形ACE斜边上的中线,所以CD=DE=AD,因此可判断△EDC是等腰三角形;
(2)先利用BA=BE=5得到CE=EB-CB=2,利用勾股定理,在Rt△ACE中计算出AE=![]() ,在Rt△ABC中计算出AC=4,利用三角形面积公式得到S△ABE=
,在Rt△ABC中计算出AC=4,利用三角形面积公式得到S△ABE=![]() ACBE=10,再证明△ECD∽△EAB,利用相似的性质求出S△ECD=2,然后利用四边形ABCD的面积=S△ABE-S△ECD进行计算..
ACBE=10,再证明△ECD∽△EAB,利用相似的性质求出S△ECD=2,然后利用四边形ABCD的面积=S△ABE-S△ECD进行计算..
解:(1)证明:∵![]() 是半圆的直径,
是半圆的直径,
∴![]() ,
,
∵![]() 的平分线交半圆于
的平分线交半圆于![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 为直角三角形
为直角三角形![]() 斜边上的中线,
斜边上的中线,
∴![]() ,
,
∴![]() 是等腰三角形;
是等腰三角形;
(2)∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
而![]() ,
,
∴![]()
![]()
![]() ,
,
∴![]() ,即
,即![]() ,
,
∴四边形![]() 的面积=
的面积=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() (k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一副扑克牌中取出6张扑克牌,分别是黑桃2、4、6,红心6、7、8.将扑克牌背面朝上分别放在甲、乙两张桌面上,先从甲桌面上任意摸出一张黑桃,再从乙桌面上任意摸出一张红心.
(1)表示出所有可能出现的结果;
(2)小黄和小石做游戏,制定了两个游戏规则:
规则1:若两次摸出的扑克牌中,至少有一张是“6”,小黄赢;否则,小石赢.
规则2:若摸出的红心牌点数是黑桃牌点数的整数倍时,小黄赢;否则,小石赢.
小黄想要在游戏中获胜,会选择哪一条规则,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
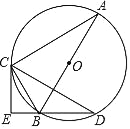
【题目】如图,AB为⊙O直径,C、D为⊙O上的点,∠ACD=2∠A,CE⊥DB交DB的延长线于点E.
(1)求证:直线CE与⊙O相切;
(2)若AC=8,AB=10,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校教师开展了“练一手好字”的活动,校委会对部分教师练习字帖的情况进行了问卷调查,问卷设置了“柳体”、“颜体”、”欧体“和”其他“类型,每位教师仅能选一项,根据调查的结果绘制了如下统计表:
类别 | 柳体 | 颜体 | 欧体 | 其他 | 合计 |
人数 | 4 | 10 | 6 | ||
占的百分比 | 0.5 | 0.25 | 1 |
根据图表提供的信息解答下列问题:
(1)这次问卷调查了多少名教师?
(2)请你补全表格.
(3)在调查问卷中,甲、乙、丙、丁四位教师选择了“柳体”,现从以上四位教师中任意选出2名教师参加学校的柳体兴趣小组,请你用画树状图或列表的方法,求选出的2人恰好是乙和丙两位教师的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠DAB=60°,AB=AD,线段BC绕点B顺时针旋转60°得到线段BE,连接AC、ED.
(1)求证:AC=DE;
(2)若DC=4,BC=6,∠DCB=30°,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
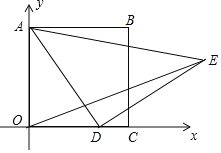
【题目】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
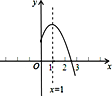
【题目】如图是二次函数![]() (a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2 ,0)和(3 ,0)之间,对称轴是x=1.对于下列结论:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m为实数);⑤ 当-1<x<3时,y>0. 其中正确结论的个数为( )
(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2 ,0)和(3 ,0)之间,对称轴是x=1.对于下列结论:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m为实数);⑤ 当-1<x<3时,y>0. 其中正确结论的个数为( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com