
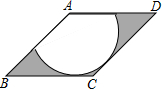
 如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )| A. | 1-$\frac{3\sqrt{2}π}{16}$ | B. | $\sqrt{2}-\frac{3π}{8}$ | C. | 1-$\frac{3π}{8}$ | D. | $\frac{3π}{8}$ |
分析 根据切线的性质得到AE⊥BC,根据投资研究得到AE=BE=$\frac{\sqrt{2}}{2}$AB,根据求概率的公式即可得到结论.
解答  解:如图,设切点为E,F,连接AE,
解:如图,设切点为E,F,连接AE,
∵以点A为圆心的扇形与BC,CD相切,
∴AE⊥BC,
∵∠B=45°,
∴AE=BE=$\frac{\sqrt{2}}{2}$AB,∠BAC=135°,
∴S菱形ABCD=BC•AE=$\frac{\sqrt{2}}{2}$AB2,
S阴影=S菱形-S扇形=$\frac{\sqrt{2}}{2}$AB2-$\frac{135•π×(\frac{\sqrt{2}}{2}AB)^{2}}{360}$=$\frac{8\sqrt{2}-3}{16}$πAB2,
∴飞镖插在阴影区域的概率=1-$\frac{3\sqrt{2}π}{16}$,
故选A.
点评 本题考查了概率的求法,菱形的性质,切线的性质,扇形的面积的计算,正确的作出辅助线是解题的关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:填空题
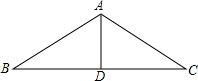 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10m,中柱AD(D为BC中点)的长是3.6m,则∠BAC=108°(用科学计算器计算,结果精确到1°).
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10m,中柱AD(D为BC中点)的长是3.6m,则∠BAC=108°(用科学计算器计算,结果精确到1°).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0或$\frac{1}{2}$ | B. | -1 | C. | -2 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
| 调整前单价x (元) | x1 | x2=6 | x3=72 | x4 | … | xn |
| 调整后单价y (元) | y1 | y2=4 | y3=59 | y4 | … | yn |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数相等 | B. | 中位数相等 | C. | 众数相等 | D. | 方差相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com