




 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源:2012-2013学年广东省茂名市愉园中学七年级下学期期中考试数学试卷(带解析) 题型:解答题
已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的数量关系,并说明你的理由.
(1)如图1,AB∥EF,BC∥DE.猜想∠1与∠2的数量关系是:_______.
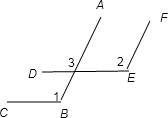
(2)如图2,AB∥EF,BC∥DE. 猜想∠1与∠2的数量关系是:_______.
(3)由(1)(2)可以得出的结论是:如果一个角的两边与另一个角的两边分别平行,那么这两个角_____ .
查看答案和解析>>
科目:初中数学 来源:2015届广东省茂名市七年级下学期期中考试数学试卷(解析版) 题型:解答题
已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的数量关系,并说明你的理由.
(1)如图1,AB∥EF,BC∥DE.猜想∠1与∠2的数量关系是:_______.

(2)如图2,AB∥EF,BC∥DE. 猜想∠1与∠2的数量关系是:_______.

(3)由(1)(2)可以得出的结论是:如果一个角的两边与另一个角的两边分别平行,那么这两个角_____ .
查看答案和解析>>
科目:初中数学 来源:江西省期中题 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:
已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的关系,并说明你的结论.
(1)如图25-1,AB∥EF,BC∥DE.∠1与∠2的关系是:____________
 理由:
理由:
(2)如图25-2,AB∥EF,BC∥DE. ∠1与∠2的关系是:
理由:
(3)由(1)(2)你得出的结论是:如果 ,那么__________________________________________________________________________.
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角度数的分别是_______________________________________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com