
【题目】如图,ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.
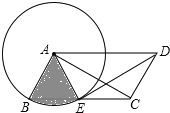
(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
【答案】(1)见解析;(2)![]() π.
π.
【解析】
试题分析:(1)由四边形ABCD是平行四边形,AB=AE,易证得四边形AECD是等腰梯形,即可得AC=DE,然后由SSS,即可证得:△AED≌△DCA;
(2)由DE平分∠ADC且与⊙A相切于点E,可求得∠EAD的度数,继而求得∠BAE的度数,然后由扇形的面积公式求得阴影部分(扇形)的面积.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴四边形AECD是梯形,
∵AB=AE,
∴AE=CD,
∴四边形AECD是等腰梯形,
∴AC=DE,
在△AED和△DCA中,
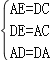 ,
,
∴△AED≌△DCA(SSS);
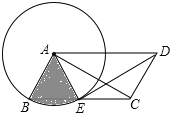
(2)解:∵DE平分∠ADC,
∴∠ADC=2∠ADE,
∵四边形AECD是等腰梯形,
∴∠DAE=∠ADC=2∠ADE,
∵DE与⊙A相切于点E,
∴AE⊥DE,
即∠AED=90°,
∴∠ADE=30°,
∴∠DAE=60°,
∴∠DCE=∠AEC=180°﹣∠DAE=120°,
∵四边形ABCD是平行四边形,
∴∠BAD=∠DCE=120°,
∴∠BAE=∠BAD﹣∠EAD=60°,
∴S阴影=![]() ×π×22=
×π×22=![]() π.
π.


科目:初中数学 来源: 题型:
【题目】将∠AOB绕点O顺时针旋转15°,得到∠COD,若∠COD=45°,则∠AOB的度数是( ).
A.15° B.30° C.45° D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在笔直的公路上行驶,两次拐弯后的方向与原来的方向相反,那么两次拐弯的角度可能是是( )
A. 第一次右拐60°,第二次左拐120°
B. 第一次左拐60°,第二次右拐60°
C. 第一次左拐60°,第二次左拐120°
D. 第一次右拐60°,第二次右拐60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级教师在讲“解直角三角形”一节时,带领一个小组登上学校教学楼上的一个平台,测量与学校毗邻的一生活小区的一栋居民楼AB的高度,平台C距离地面D高10米,在C处测得居民楼楼底B的俯角为22.5°,楼顶端A的仰角为60°,测完后,记录好数据,回到教师,将示意图画在黑板上,如图所示,要求全班学生按示意图,求出居民楼AB的高度.(最后结果精确到0.1)(参考数据:tan22.5°=![]() ﹣1,
﹣1,![]() =1.73,
=1.73,![]() =1.41)
=1.41)
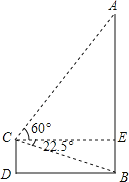
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com