
����Ŀ��С��ҡ�С���ҡ�ѧУ������ͬһ����ֱ�Ĺ�·�ԣ����Ե���·�ľ�����Բ��ƣ���ÿ������7����С�춼��Ӽҳ�����ÿ����60���ٶ��ߵ�������600��С���ң�Ȼ��������С��ͬ�����ٶ�ʱ��7��30��У�����ij������7�����С���ڼҵ�С���ʱ��ͻȻ��������ֵ��Լ�ֵ��ɨ���ˣ����Ծ���ÿ����60���ٶ�����ѧУ��ȥ����������ٺ�С����ͣ�С������С����һ��С�����ڼң������뵽С��������ֵ������ͣ����˼��ʱ����Բ��ƣ�������������ÿ����100���ٶ�ȥС��������֮��ľ���y���ף���С��������ʱ��x���֣�֮��ĺ�����ϵ����ͼ��ʾ�����ʵ�С����С��ʱ��ѧУ����_____�ף�
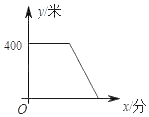
���𰸡�200
��������
��������ͺ���ͼ���е����ݿ�����õ�С����С��ʱ��ѧУ���ж���ǧ�ף�������Խ����
�⣺��С��ӵ�С���ҵ���С���õ�ʱ��Ϊa���ӣ�������ɵã�
400+60a��100a��
��ã�a��10��
��С��ӵ�С���ҵ���С���õ�ʱ��Ϊ10���ӣ�
��С��7��00�Ӽҳ�������ѧУ7��30��
��С��Ӽҵ�ѧУ�õ�ʱ��Ϊ��30���ӣ�
�൱С����С��ʱ��ѧУ���У�60��30��600��100��10��200���ף���
�ʴ�Ϊ��200��


 ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��CEƽ�֡�ACD��AEƽ�֡�BAC����EAC+��ACE=90��
��1�����ж�AB��CD��λ�ù�ϵ��˵�����ɣ�
��2����ͼ2������E=90����AB��CD��λ�ù�ϵ���ֲ��䣬�ƶ�ֱ�Ƕ���E��ʹ��MCE=��ECD����ֱ�Ƕ���E���ƶ�ʱ���ʡ�BAE���MCD�����ȷ����������ϵ����˵�����ɣ�
��3����ͼ3��PΪ�߶�AC��һ���㣬��QΪֱ��CD��һ������AB��CD��λ�ù�ϵ���ֲ��䣬����Q������CD���˶�ʱ����C���⣩��CPQ+��CQP���BAC�к�������ϵ��������۲�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵ�A��ʾ����Ϊ��3����B��ʾ����Ϊ3�����������ϴ��ڵ�P��ʹ��AP+BP=m����Ƶ�PΪ��A��B����m�����µ��������磬ԭ��O��ʾ����Ϊ0����AO+BO=3+3=6����Ƶ�OΪ��A�͵�B����6�����µ��������������涨������������⣺
��1������C���������ϱ�ʾ����Ϊ��5����CΪ��A�͵�B����m�����µ�������m= ��
��2������D�������ϵ�A�͵�B����8�����µ��������D��ʾ������
��3����ͼ�������ϵ�E�͵�F�ֱ��ʾ�����ǩ�2��4������G�ǵ�E�͵�F����m�����µ�����������GE=3GF����m��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱���������ѧУ��չ��ȫУ�Ե�������������ǰ�������ȡ����ѧ����������ǵ������������ͼ��ʾ�����ݰ�����˵㲻�����Ҷ˵㣬��ȷ��0.1��������ٴμ���ⲿ��ѧ������������������ʾ
���� | Ƶ�� |
4.0��x��4.2 | 2 |
4.2��x��4.4 | 3 |
4.4��x��4.6 | 5 |
4.6��x��4.8 | 8 |
4.8��x��5.0 | 17 |
5.0��x��5.2 | 5 |
��1��������ȡ��ѧ��������
��2���������ﵽ4.8������Ϊ��꣬����ǰ��Уѧ������������ʣ�
��3����ѡ���ʵ���ͳ��������������ͬ�ĽǶ����������������Ч����
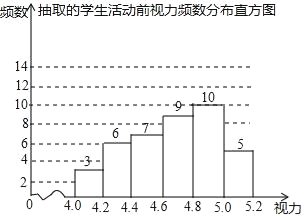
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı�BC�Ƶ�C��ʱ����ת90�㵽CE������AC��DE��BE��AC��DE�ཻ��F�����AFD��_____��
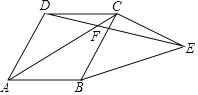
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ҫ����һ��Բ����ˮ�أ���ˮ�����봹ֱ�ڵ��氲װһ������OA��OǡΪˮ�����ģ����������Ӷ���A������ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·������.�ڹ�OA����һƽ���ϣ�����ƽ��ֱ������ϵ����ͼ����ˮ������ĸ߶�y��m����ˮƽ����x��m��֮��Ĺ�ϵʽ��![]() �������н��ۣ���1������OA�ĸ߶�Ϊ3m����2�������ˮ��������1m���ﵽ���߶ȣ���3�������ˮ����ˮƽ������߶���4m����4��ˮ�صİ뾶����Ҫ3m����ʹ�����ˮ�����������ڳ���.������ȷ���У� ��
�������н��ۣ���1������OA�ĸ߶�Ϊ3m����2�������ˮ��������1m���ﵽ���߶ȣ���3�������ˮ����ˮƽ������߶���4m����4��ˮ�صİ뾶����Ҫ3m����ʹ�����ˮ�����������ڳ���.������ȷ���У� ��
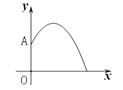
A. 1�� B. 2�� C. 3�� D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�߳�Ϊ3����E��AB������BE=1����P��Q�ֱ��DZ�BC��CD�Ķ��㣨�����붥���غϣ������ı���AEPQ���ܳ�ȡ��Сֵʱ���ı���AEPQ������ǣ�������
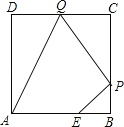
A. 3 B. 5 C. 4 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Rt��ABC�У���C=90�㣬AC=6��BC=8������P�ӵ�A��ʼ�ر�AC���C��1����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�������P��PD��BC����AB�ڵ�D������PQ�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1��ֱ���ú�t�Ĵ���ʽ�ֱ��ʾ��QB=�� ����PD=�� ����
��2���Ƿ����t��ֵ��ʹ�ı���PDBQΪ���Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ���̽����θı�Q���ٶȣ������˶�����ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȣ�
��3����ͼ2���������˶������У�����߶�PQ�е�M��������·������
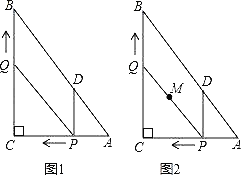
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com