
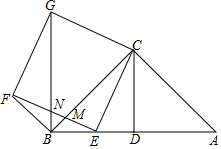
 已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.
已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.分析 (1)根据SAS即可证明;
(2)只要证明△NBE∽△EDC,可得$\frac{BN}{ED}$=$\frac{BE}{CD}$,可得$\frac{y}{x}$=$\frac{2-x}{2}$,由此即可解决问题;
(3)在CD上取一点K,使得DE=DK=2$\sqrt{2}$-2,首先证明KE=KC,再证明△BEF≌△KEC即可解决问题;
解答 (1)证明:∵四边形EFGC是正方形,
∴CG=CE,∠GCE=∠GFE=∠FEC=90°,
∵∠ACB=∠GCE=90°,
∴∠GCB=∠ECA,
∵GC=CE,CB=CA,
∴△CAE≌△CBG.
(2)解:∵CB=CA,CD⊥AB,∠ACB=90°,
∴CD=BD=AD=2,∠CBA=∠A=45°,
∵△CAE≌△CBG,
∴∠CBG=∠A=45°,
∴∠GBA=∠GBC+∠CBA=90°,
∵∠BEN+∠BNE=90°,∠BEN+∠CED=90°,
∴∠BNE=∠CED,∵∠EBN=∠CDE=90°,
∴△NBE∽△EDC,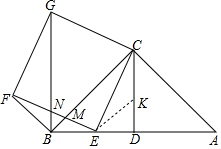
∴$\frac{BN}{ED}$=$\frac{BE}{CD}$,
∴$\frac{y}{x}$=$\frac{2-x}{2}$,
∴y=-$\frac{1}{2}$(x-1)2+$\frac{1}{2}$,
∵-$\frac{1}{2}$<0,
∴x=1时,y的最大值为$\frac{1}{2}$.
(3)解:在CD上取一点K,使得DE=DK=2$\sqrt{2}$-2,
∴EK=4-2$\sqrt{2}$,
∵CK=CD-DK=2-(2$\sqrt{2}$-2)=4-2$\sqrt{2}$,
∴KC=EK,
∵∠EKD=∠KED=45°,
∴∠KEC=∠KCE=22.5°,
∴∠CED=67.5°,
∴∠FEB=90°-67.5°=22.5°,
∵BE=BD-DE=4-2$\sqrt{2}$=EK,CE=EF,∠BEF=∠ECK,
∴△BEF≌△KEC,
∴∠EFB=∠ECK=22.5°.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 4$\sqrt{2}$ | C. | 4 | D. | -4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{3x}$ | C. | $\sqrt{{2x}^{3}}$ | D. | $\sqrt{\frac{5}{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
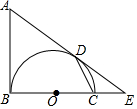 如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD、BC的延长线相交于点E.
如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD、BC的延长线相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC内接于⊙O,⊙O的半径为5,sin∠B=$\frac{3}{5}$,点D在边AC上,在弧BC上取一点E.使得∠CDE=∠ABC.且AE=$\sqrt{3}$DE.则CD的长为( )
如图,△ABC内接于⊙O,⊙O的半径为5,sin∠B=$\frac{3}{5}$,点D在边AC上,在弧BC上取一点E.使得∠CDE=∠ABC.且AE=$\sqrt{3}$DE.则CD的长为( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com