
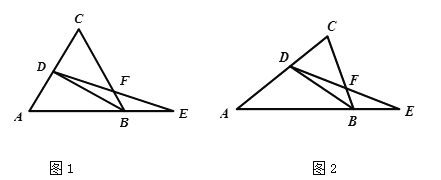
【题目】在△ABC中,AB=AC,∠ABC的平分线交AC于点D,在AB的延长线上截取BE,使BE=CD,连接DE交BC于点F.
(1)如图1,当∠CAB=60°时,若AB=2,求DE的长度;
(2)如图2,当∠CAB≠60°时,求证:BE=2BF.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)如图1中,作DH⊥AB于H.在Rt△DEH中,求出DH、EH,利用勾股定理即可解决问题;
(2)如图2中,作DH∥AB交BC于H,连接EH.只要证明四边形DBEH是平行四边形,再证明BH=BE,即可解决问题.
试题解析:解:(1)如图1中,作DH⊥AB于H.
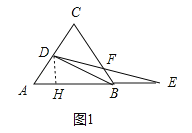
∵AC=AB,∠CAB=60°,∴△ABC是等边三角形,∴AB=BC=AC=2,∠A=60°.∵BD平分∠ABC,∴AD=DC=1.在Rt△ADH中,∵∠ADH=30°,AD=1,∴AH=![]() ,DH=
,DH=![]() .∵BE=CD=1,∴EH=BH+BE=
.∵BE=CD=1,∴EH=BH+BE=![]() .在Rt△DHE中,DE=
.在Rt△DHE中,DE=![]() =
=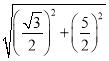 =
=![]() .
.
(2)如图2中,作DH∥AB交BC于H,连接EH.
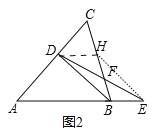
∵AB=AC,∴∠C=∠ABC.∵DH∥AB,∴∠DHC=∠ABC=∠C,∴DH=DC.∵DC=BE,∴四边形DBEH是平行四边形,∴FH=FB,BD∥EH,∴∠BHE=∠DBH,∠DBA=∠BEH.∵∠DBA=∠DBC,∴∠BHE=∠BEH,∴BH=BE,∴BE=2BF.


科目:初中数学 来源: 题型:
【题目】图![]() 是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数
是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数![]() ,
, ![]() ,
, ![]() ,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为
,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为![]() (如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图
(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图![]() 是背面完全一样、牌面数字分别是
是背面完全一样、牌面数字分别是![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌的牌面数字记为
的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌的牌面数字记为![]() .计算
.计算![]() 的值.
的值.


(![]() )用树状图或列表法求
)用树状图或列表法求![]() 的概率.
的概率.
(![]() )甲乙两人玩游戏,规定:当
)甲乙两人玩游戏,规定:当![]() 是正数时,甲胜;否则,乙胜,你认为这个游戏规则对甲乙双方公平吗?请说明理由.
是正数时,甲胜;否则,乙胜,你认为这个游戏规则对甲乙双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
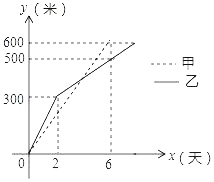
【题目】甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(单位:米)与挖掘时间x(单位:天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③当x=4时,甲、乙两队所挖管道长度相同;④甲队比乙队提前2天完成任务.正确的是_____(直接填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
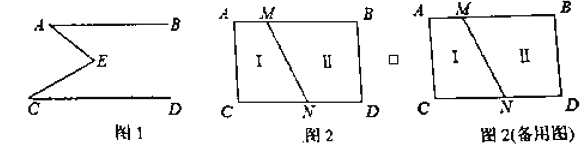
【题目】如图1,![]() ,点
,点![]() 是直线
是直线![]() 、
、![]() 之间的一点,连接
之间的一点,连接![]() 、
、![]() .
.
(1)问题发现:
①若![]() ,
,![]() ,则
,则![]() ___________.
___________.
②猜想图1中![]() 、
、![]() 、
、![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
(2)拓展应用:
如图2,![]() ,线段
,线段![]() 把
把![]() 这个封闭区域分为Ⅰ、Ⅱ两部分(不含边界),点
这个封闭区域分为Ⅰ、Ⅱ两部分(不含边界),点![]() 是位于这两个区域内的任意一点,请直接写出
是位于这两个区域内的任意一点,请直接写出![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
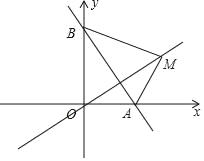
【题目】如图,在平面直角坐标系中,A(p,0),B(0,q),且p、q满足(p﹣2)2+![]() =0.
=0.
(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,且△ABM是以AB为底的等腰直角三角形,求m值.
查看答案和解析>>
科目:初中数学 来源: 题型:
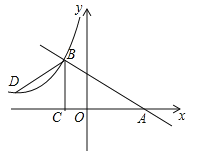
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△ADE都是直角三角形,∠C=∠AED=![]() ,点E在AB上,∠D=
,点E在AB上,∠D=![]() .如果△ABC经顺时针旋转后能与△ADE重合,那么旋转中心是点______,旋转了______度
.如果△ABC经顺时针旋转后能与△ADE重合,那么旋转中心是点______,旋转了______度

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4.5>=5,<-1.5>=-1.解决下列问题.
(1)[-4.5]=_____;<3.5>=________;
(2)若[x]=2,则x的取值范围是________;若<y>=-1,则y的取值范围是_______.
(3)若![]() ,则x为_________.
,则x为_________.
(4)已知x、y满足方程组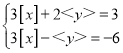
![]() ,求x、y的取值范围.
,求x、y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了某校七年级学生对![]() 《最强大脑》、
《最强大脑》、![]() 《朗读者》、
《朗读者》、![]() 《中国诗词大会》、
《中国诗词大会》、![]() 《极限挑战》四个电视节目的喜爱情况,随机抽取了
《极限挑战》四个电视节目的喜爱情况,随机抽取了![]() 位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2)
位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2)
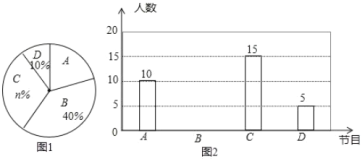
根据统计图提供的信息,回答下列问题:
(1)![]() ______,
______,![]() ______.
______.
(2)在图1中,喜爱《朗读者》节目所对应的扇形的圆心角度数是______度;
(3)请根据以上信息直接在答题卡中补全图2的条形统计图;
(4)已知该校七年级共有420位学生,那么他们最喜欢《中国诗词大会》这个节目的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com