
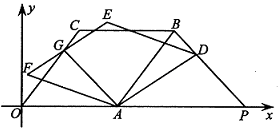
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C在第一象限,tan∠AOC=![]() ,将菱形绕点A按顺时针方向旋转角α(0°<α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG。
,将菱形绕点A按顺时针方向旋转角α(0°<α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG。
(1)求点B的坐标;
(2)当OG=4时,求AG的长;
(3)求证:GA平分∠OGE;
(4)连结BD并延长交![]() 轴于点P,当点P的坐标为(12,0)时,求点G的坐标。
轴于点P,当点P的坐标为(12,0)时,求点G的坐标。
【答案】(1)(8,4);(2)![]() ;(3)(
;(3)(![]() ).
).
【解析】
试题分析:(1)如图1,过点B作BH⊥x轴于点H,由已知可得∠BAH=∠COA,在Rt△ABH中,tan∠BAH=tan∠AOC=![]() ,AB=5,可求得BH=4,AH=3,所以OH=8,即可得点B的坐标为(8,4);(2)如图1,过点A作AM⊥OC于点M,在Rt△AOM中,tan∠AOC=
,AB=5,可求得BH=4,AH=3,所以OH=8,即可得点B的坐标为(8,4);(2)如图1,过点A作AM⊥OC于点M,在Rt△AOM中,tan∠AOC=![]() ,OA=5,可求得AM=4,OA=3,所以GM=1,再由勾股定理即可求得AG=
,OA=5,可求得AM=4,OA=3,所以GM=1,再由勾股定理即可求得AG=![]() ;(3)如图1,过点A作AN⊥EF轴于点N,易证△AOM≌△AFN,根据全等三角形的性质可得AM=AN,再由角平分线的判定可得GA平分∠OGE;(4)如图2,过点G作GQ⊥x轴于点Q,先证△GOA∽△BAP,根据相似三角形的性质求得GQ=
;(3)如图1,过点A作AN⊥EF轴于点N,易证△AOM≌△AFN,根据全等三角形的性质可得AM=AN,再由角平分线的判定可得GA平分∠OGE;(4)如图2,过点G作GQ⊥x轴于点Q,先证△GOA∽△BAP,根据相似三角形的性质求得GQ=![]() ,再由锐角三角函数求得OQ=
,再由锐角三角函数求得OQ=![]() ,即可得点G的坐标为(
,即可得点G的坐标为(![]() ).
).
试题解析:
(1)如图1,过点B作BH⊥x轴于点H,
∵四边形OABC为菱形,∴OC∥AB,
∴∠BAH=∠COA.
∵tan∠AOC=![]() ,
,
∴tan∠BAH=![]() .
.
又∵在直角△BAH中,AB=5,
∴BH=3![]() AB=4,AH=
AB=4,AH=![]() AB=3,
AB=3,
∴OH=OA+AH=5+3=8,
∴点B的坐标为(8,4);
(2)如图1,过点A作AM⊥OC于点M,
在直角△AOM中,∵tan∠AOC=![]() ,OA=5,
,OA=5,
∴AM=![]() OA=4,OM=
OA=4,OM=![]() OA=3,
OA=3,
∵OG=4,
∴GM=OG-OM=4-3=1,
∴AG=![]() ;
;
(3)如图1,过点A作AN⊥EF于点N,
∵在△AOM与△AFN中,
∠AOM=∠F,OA=FA,∠AMO=∠ANF=90°,
∴△AOM≌△AFN(ASA),
∴AM=AN,
∴GA平分∠OGE.
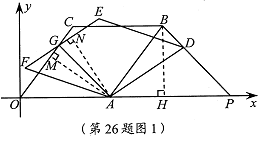
(4)如图2,过点G作GQ⊥x轴于点Q,
由旋转可知:∠OAF=∠BAD=α.
∵AB=AD,
∴∠ABP=![]() ,
,
∵∠AOT=∠F,∠OTA=∠GTF,
∴∠OGA=∠EGA=1![]() ,
,
∴∠OGA=ABP,
又∵∠GOA=∠BAP,
∴△GOA∽△BAP,
∴![]() ,
,
∴GQ=![]() ×4=
×4=![]() .
.
∵tan∠AOC=![]() ,
,
∴OQ=![]() ×
×![]() =
=![]() ,
,
∴G(![]() ,
,![]() ).
).



科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A. 在同圆或等圆中,同弧或等弧所对的圆周角相等
B. 平分弦的直径垂直于弦
C. 两条平行线间的距离处处相等
D. 正方形的两条对角线互相垂直平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F是□ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).
(1)连结_____;
(2)猜想:_____=_____;
(3)证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A、B两种上网学习的月收费方案:
A方案:月租7元,可上网25小时,若超时,超出部分按每分钟0.01元收费;
B方案:月租10元,可上网50小时,若超时,超出部分按每分钟0.01元收费;
设每月上网学习时间为![]() 小时.
小时.
(1)当![]() >50时,用含有x的代数式分别表示A、B两种上网的费用;
>50时,用含有x的代数式分别表示A、B两种上网的费用;
(2)当x=100时,分别求出两种上网学习的费用.
(3)若上网40小时,选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,CE是∠DCB的平分线,F是AB的中点,AB=6,BC=5,则AE:EF:FB为( )

A. 1:2:3 B. 2:1:3 C. 3:2:1 D. 3:1:2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com