
【题目】如图,一农户要建一个矩形猪舍,猪舍的一边利用现有的住房墙,另外三边用 25m 长得建筑材料围成,为方便进出,在垂直于住房墙的一边留一个小门.
(1)如果住房墙长 12 米,门宽为 1 米,所围矩形猪舍的长、宽分别为多少时,猪舍面积为 80m2?
(2)如果住房墙长 12 米,门宽为 1 米,当 AB 边长为多少时,猪舍的面积最大?最大面积是多少?
(3)如果住房墙足够长,门宽为a 米,设 AB=x 米,当 6.5≤x≤7 时,猪舍的面积 S 先增大,后减小,直接写出a 的范围.

【答案】(1)长是10米、宽分8米时; (2)当AB边长为7米时,猪舍的面积最大,最大面积是84平方米;(3)1<a<3.
【解析】
(1)根据题意可以设平行于墙的边长为x米,然后列出相应的方程,注意解得的x的值不能大于12米;
(2)设平行于墙的长,然后列出相应的S关于x的函数关系式,从而可以求得AB边长为多少时,猪舍的面积最大,最大面积是多少;
(3)根据题意可以求得S关于x的关系系和列出相应的不等式,从而可以求得a的取值范围.
解:(1)平行于围墙的边长为x米,
x![]() =80,
=80,
解得,x1=10,x2=16(舍去)
∴![]() =8,
=8,
即所围矩形猪舍的长是10米、宽分8米时,猪舍面积为80平方米;
(2)设平行于围墙的边长为x米,猪舍的面积为S平方米,
S=x![]() =
=![]() (x13)2+
(x13)2+![]() ,
,
∵墙长12米,
∴当x=12时,S取得最大值,此时S=84,
![]() =7,
=7,
即当AB边长为7米时,猪舍的面积最大,最大面积是84平方米;
(3)由题意可得,
S=x(25+a-2x)=2(x![]() )2+
)2+![]() ,
,
∵当6.5≤x≤7时,猪舍的面积S先增大,后减小,
∴6.5<![]() <7,
<7,
解得,1<a<3,
即a的取值范围是1<a<3.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
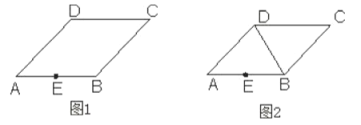
【题目】在菱形![]() 中,点
中,点![]() 是边
是边![]() 的中点,试分别在下列两个图形中按要求使用无刻度的直尺画图.
的中点,试分别在下列两个图形中按要求使用无刻度的直尺画图.
(1)在图1中,过点![]() 画
画![]() 的平行线;
的平行线;
(2)在图2中,连接![]() ,在
,在![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() ,
,![]() 的距离之和最短.
的距离之和最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5)
(1)求该函数的关系式;
(2)求该函数图象与坐标轴的交点坐标;
(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:![]() >0.
>0.
解:设![]() =0,解得:
=0,解得:![]() =0,
=0,![]() =5,则抛物线y=
=5,则抛物线y=![]() 与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=
与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=![]() 的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即
的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即![]() >0,所以,一元二次不等式
>0,所以,一元二次不等式![]() >0的解集为:x<0或x>5.
>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式![]() <0的解集为 .
<0的解集为 .
(3)用类似的方法解一元二次不等式:![]() >0.
>0.
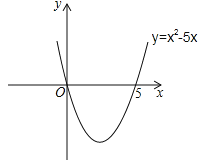
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为假命题的是( )
A.三条边分别对应相等的两个三角形全等B.三角形的一个外角大于与它相邻的内角
C.角平分线上的点到角两边的距离相等D.有一个角是![]() 的等腰三角形是等边三角形
的等腰三角形是等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
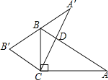
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以直角顶点
,以直角顶点![]() 为旋转中心,将
为旋转中心,将![]() 逆时针旋转到
逆时针旋转到![]() 的位置,其中
的位置,其中![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的对应点,且点
的对应点,且点![]() 在斜边
在斜边![]() 上,直角边
上,直角边![]() 交
交![]() 于
于![]() ,则旋转角
,则旋转角![]()
![]() 的度数为________.
的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
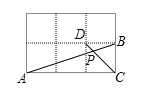
【题目】(2016四川省自贡市)如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则![]() 的值=______,tan∠APD的值=______.
的值=______,tan∠APD的值=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
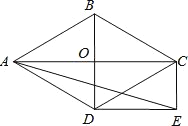
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C. D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求EA的长。
时,求EA的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com