
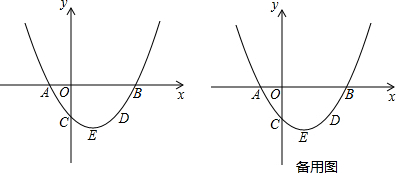
分析 (1)利用分解因式法解方程x2-8x+12=0即可得出x的值,再根据OB>OA即可得出点A、B的坐标;
(2)根据抛物线过x轴上的两点AB,可设抛物线的解析式为:y=a(x+2)(x-6)(a≠0),再由点C的坐标利用待定系数法即可求出经过A,B,C三点的抛物线的关系式;
(3)①设点M的坐标为(0,m),根据抛物线的关系式即可得出点E的坐标,由两点间的距离公式可求出线段CE、CM、ME的长度,再根据等腰三角形的性质分三种情况考虑,由边相等得出关于m的方程,解方程即可得出m值,从而得出点M的坐标;
②作点E关于y轴对称的点E′,作点D关于x轴对称的点D′,连接D′E′交x轴于点N,交y轴于点M,此时以D、E、M、N位顶点的四边形的周长最小.根据点C的坐标可得出点D的坐标,根据对称的性质即可得出点D′、E′的坐标,由此即可求出四边形周长的最小值,再根据点D′、E′的坐标,利用待定系数法即可求出直线D′E′的解析式,由此即可得出点M、N的坐标.
解答 解:(1)∵x2-8x+12=0,
∴(x-2)(x-6)=0,
解得:x1=2,x2=6,
∵OB>OA,
∴OA=2,OB=6,
∴点A的坐标为(-2,0),点B的坐标为(6,0).
(2)设抛物线的解析式为:y=a(x+2)(x-6)(a≠0),
将C(0,-3)代入得:-3=-12a,
解得:a=$\frac{1}{4}$,
∴经过A,B,C三点的抛物线的关系式为:y=$\frac{1}{4}$(x+2)(x-6)=$\frac{1}{4}$x2-x-3.
(3)①依据题意画出图形,如图1所示.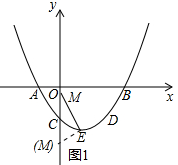
设点M的坐标为(0,m),
∵抛物线的关系式为y=$\frac{1}{4}$x2-x-3=$\frac{1}{4}$(x-2)2-4,
∴点E(2,-4),
∴CE=$\sqrt{5}$,CM=|m+3|,ME=$\sqrt{4+(m+4)^{2}}$.
△CEM是等腰三角形分三种情况:
当CE=CM时,有$\sqrt{5}$=|m+3|,
解得:m=$\sqrt{5}$-3或m=-$\sqrt{5}$-3,
此时点M的坐标为(0,$\sqrt{5}$-3)或(0,-$\sqrt{5}$-3);
当CE=ME时,有$\sqrt{5}$=$\sqrt{4+(m+4)^{2}}$,
解得:m=-3(舍去)或m=-5,
此时点M的坐标为(0,-5);
当CM=ME时,有|m+3|=$\sqrt{4+(m+4)^{2}}$,
解得:m=-$\frac{11}{2}$,
此时点M的坐标为(0,-$\frac{11}{2}$).
综上可知:当△CEM是等腰三角形时,点M的坐标为(0,$\sqrt{5}$-3)、(0,-$\sqrt{5}$-3)、(0,-5)或(0,-$\frac{11}{2}$).
②四边形DEMN有最小值.
作点E关于y轴对称的点E′,作点D关于x轴对称的点D′,连接D′E′交x轴于点N,交y轴于点M,此时以D、E、M、N位顶点的四边形的周长最小,如图2所示.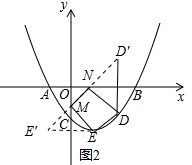
∵点C(0,-3),点E(2,-4),
∴点D(4,-3),DE=$\sqrt{(4-2)^{2}+[-3-(-4)]^{2}}$=$\sqrt{5}$.
∵E、E′关于y轴对称,D、D′关于x轴对称,
∴EM=E′M,DN=D′N,点E′(-2,-4),点D′(4,3),
∴EM+MN+DN=D′E′=$\sqrt{[4-(-2)]^{2}+[3-(-4)]^{2}}$=$\sqrt{85}$,
∴C四边形DEMN=DE+EM+MN+DN=$\sqrt{5}$+$\sqrt{85}$.
设直线D′E′的解析式为y=kx+b,
则有$\left\{\begin{array}{l}{3=4k+b}\\{-4=-2k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{7}{6}}\\{b=-\frac{5}{3}}\end{array}\right.$,
∴直线D′E′的解析式为y=$\frac{7}{6}$x-$\frac{5}{3}$.
令y=$\frac{7}{6}$x-$\frac{5}{3}$中x=0,则y=-$\frac{5}{3}$,
∴点M(0,-$\frac{5}{3}$);
令y=$\frac{7}{6}$x-$\frac{5}{3}$中y=0,则$\frac{7}{6}$x-$\frac{5}{3}$=0,解得:x=$\frac{10}{7}$,
∴点N($\frac{10}{7}$,0).
故以D、E、M、N位顶点的四边形的周长有最小值,最小值为$\sqrt{5}$+$\sqrt{85}$,此时点M的坐标为(0,-$\frac{5}{3}$),点N的坐标为($\frac{10}{7}$,0).
点评 本题考查了解一元二次方程、待定系数法求函数解析式、等腰三角形的性质以及轴对称中的最短路径问题,解题的关键是:(1)利用分解因式法解方程;(2)利用待定系数法求出函数解析式;(3)①分情况讨论;②找出点M、N的位置.本题属于难题,解题过程较繁琐,解决该题型题目时,找出点的坐标,利用待定系数法求出函数解析式是关键.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
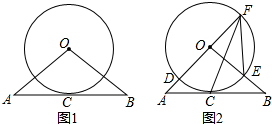
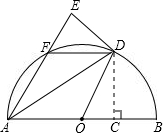 如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆O于点D,将△ACD沿AD翻折得到△AED,AE交半圆O于点F,连接DF、OD.
如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆O于点D,将△ACD沿AD翻折得到△AED,AE交半圆O于点F,连接DF、OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
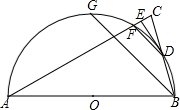 如图,已知△ABC中,AB=AC,∠A=30°,AB=16,以AB为直径的⊙O与BC边相交于点D,与AC交于点F,过点D作DE⊥AC于点E.
如图,已知△ABC中,AB=AC,∠A=30°,AB=16,以AB为直径的⊙O与BC边相交于点D,与AC交于点F,过点D作DE⊥AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com