
 (1)已知:
(1)已知: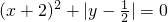 ,求代数式(2x-3y-2xy)-(x-4y+xy)的值.
,求代数式(2x-3y-2xy)-(x-4y+xy)的值.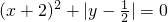 ,
, =0,
=0, ,
,
 -3×(-2)×
-3×(-2)× =
= ;
; ×3×4=6.
×3×4=6.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
| a-2 |
| 2-a |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:
 在一次探究性活动中,教师提出了问题:已知矩形的长和宽分别是2和1,是否存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2倍?设所求矩形的长和宽分别为x,y
在一次探究性活动中,教师提出了问题:已知矩形的长和宽分别是2和1,是否存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2倍?设所求矩形的长和宽分别为x,y| 4 |
| x |
| 4 |
| x |
|
|
查看答案和解析>>
科目:初中数学 来源:2013届浙江省杭州市高桥初中教育集团九年级第二学期期初质量检测数学卷(带解析) 题型:解答题
已知 、
、 均为锐角,且
均为锐角,且 ,
, 。求
。求 的度数。
的度数。
小聪、小明、小慧三位同学都通过构造一个几何图形,使这个代数计算问题快速、简捷地得到了解决,请你思考他们的方法,选择其中一个图形,解答上述问题。(也可以自己构造一个不同的图形,并完成解答)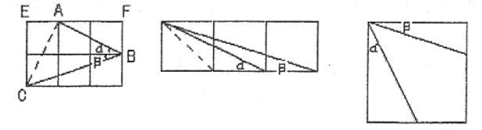
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com