
����Ŀ����ͼ������ʦ�����һ��̽���ܸ�ƽ��������ʵ�飺��һ������������ƽ����������߹̶�����A�з���һ��������ұ����B(�������ƶ�)�з���һ�����������룬ʹ����������ƽ�⣮�ı�����B���O�ľ���x(cm)���۲�����B�����������y(g)�ı仯�����ʵ�����ݼ�¼���±���
![]()

(1)�²�y��x֮��ĺ�����ϵ�����������ϵʽ��������֤��
(2)�����������Ϊ24 gʱ�������B���O�ľ����Ƕ��٣�
(3)�������B�����ƶ�ʱ��Ӧ�������B�����ӻ��Ǽ������룿
���𰸡���1����������(2) 12.5 cm��(3)��������
��������
��1���۲�ɵã�x��y�ij˻�Ϊ��ֵ300����y��x֮��ĺ�����ϵΪ�����������������ݴ����ô���ϵ�����ɵ÷����������Ĺ�ϵʽ��
��2����x=24�������ʽ��⣬�ɵô𰸣�
��3�����ú��������Լ��ɵó������Ż����B��O��ľ��벻�����������ʾ��Ӧ�ò��ϼ�С��
�⡡(1)�ɱ���²�y��x֮��ĺ�����ϵΪ������������
����y��![]() (k��0)��
(k��0)��
��x��10��y��30���룬��k��300��
��y��![]() ��
��
��������������֤���ʺϣ�
��y��x�ĺ�����ϵʽΪy��![]() ��
��
(2)��y��24����y��![]() ����x��12.5��
����x��12.5��
�൱���������Ϊ24 gʱ�������B���O�ľ�����12.5 cm.
(3)���ݷ����������������ԣ����ɵó������Ż����B��O��ľ��벻�ϼ�С�������ʾ���������
��Ӧ�������룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪֱ�������Σ���C=90�㣬BC=2cm����A=30�����ı���DEFGΪ���Σ�DE=2![]() cm��EF=6cm���ҵ�C��B��E��F��ͬһ��ֱ���ϣ���B���E�غϣ�Rt��ABC��ÿ��1cm���ٶ��ؾ���DEFG�ı�EF����ƽ�ƣ�����C���F�غ�ʱֹͣ����Rt��ABC�����DEFG���ص����ֵ����Ϊycm2���˶�ʱ��xs���ܷ�ӳycm2��xs֮�亯����ϵ�Ĵ���ͼ���ǣ�������
cm��EF=6cm���ҵ�C��B��E��F��ͬһ��ֱ���ϣ���B���E�غϣ�Rt��ABC��ÿ��1cm���ٶ��ؾ���DEFG�ı�EF����ƽ�ƣ�����C���F�غ�ʱֹͣ����Rt��ABC�����DEFG���ص����ֵ����Ϊycm2���˶�ʱ��xs���ܷ�ӳycm2��xs֮�亯����ϵ�Ĵ���ͼ���ǣ�������

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C����������y=ax2��2amx+am2+2m��5�����Щ�![]() ��a��0���ϣ�AB��x�ᣬ��ABC=135������AB=4��
��a��0���ϣ�AB��x�ᣬ��ABC=135������AB=4��
��1����գ������ߵĶ�������Ϊ ���ú�m�Ĵ���ʽ��ʾ����
��2������ABC��������ú�a�Ĵ���ʽ��ʾ����
��3������ABC�����Ϊ2����2m��5��x��2m��2ʱ��y�����ֵΪ2����m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD���������в�����ͼ������AΪԲ�ģ�AC��Ϊ�뾶������AD���ӳ����ڵ�E������EΪԲ�ģ�EC��Ϊ�뾶������DE���ӳ����ڵ�F���۷ֱ���C��FΪԲ�ģ�����![]() CF�ij�Ϊ�뾶�����������ཻ�ڵ�N����������EN��������ͼ������ACB��72�㣬���FEN�Ķ���Ϊ��������
CF�ij�Ϊ�뾶�����������ཻ�ڵ�N����������EN��������ͼ������ACB��72�㣬���FEN�Ķ���Ϊ��������
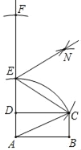
A. 54�� B. 63�� C. 72�� D. 75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+bx+c��a��0��ͼ���һ������ͼ��ʾ����Գ���Ϊx��2����x���һ�������ǣ���1��0���������½��ۣ���abc��0����4a��2b+c��0����4a+b��0����������x�����һ�������ǣ�5��0�������㣨��3��y1������6��y2�������������ϣ���y1��y2��������ȷ����_____����ֻ����ţ�
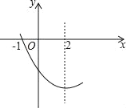
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��ABC��ƽ����BE��AC�ڵ�E������E��ֱ��BE�Ĵ��߽�AB�ڵ�F����O�ǡ�BEF�����Բ��
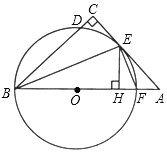
��1����֤��AC�ǡ�O�����ߣ�
��2������E��EH��AB�ڵ�H����֤��EFƽ�֡�AEH��
��3����֤��CD=HF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��x2��3x+c��y��Ľ���Ϊ��0��2����������˵����ȷ���ǣ�������
A. �����߿�������
B. ��������x��Ľ���Ϊ����1��0������3��0��
C. ��x��1ʱ��y�����ֵΪ0
D. �����ߵĶԳ�����ֱ��x��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��C��D���ڡ�O�ϣ�����C��AC��BD��OB�ӳ����ڵ�A������CD���ҡ�CDB=��OBD=30����DB=![]() cm��
cm��
��1����֤��AC�ǡ�O�����ߣ�
��2��������CD��BD�뻡BC��Χ�ɵ���Ӱ���ֵ�������������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB�뺯��y��![]() ��x��0����ͼ���ڵ�A��m��2����B��2��n��������A��ACƽ����x�ύy���ڵ�C����y�Ḻ������ȡһ��D��ʹOD��
��x��0����ͼ���ڵ�A��m��2����B��2��n��������A��ACƽ����x�ύy���ڵ�C����y�Ḻ������ȡһ��D��ʹOD��![]() OC������ACD�������6������BC��
OC������ACD�������6������BC��
��1����m��k��n��ֵ��
��2������ABC�������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com