
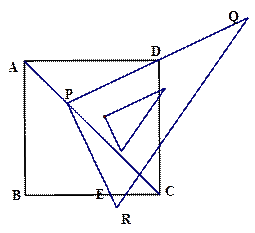
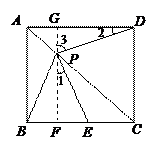
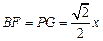 ,
,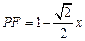 ………7分
………7分 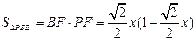
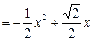 .
. 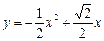 (
(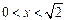 )………8分
)………8分 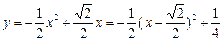 .
. 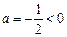 ,
,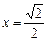 时,
时,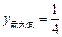 ………9分 解析:
………9分 解析:

科目:初中数学 来源: 题型:
(本小题满分12分)如图所示,在梯形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为直径的
为直径的![]() 与
与![]() 相切于
相切于![]() .已知
.已知![]() ,边
,边![]() 比
比![]() 大6.
大6.

(1)求边 、
、 的长.
的长.
(2)在直径 上是否存在一动点
上是否存在一动点 ,使以
,使以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出
相似?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
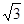 ,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线
,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线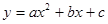 过点A、E、D.
过点A、E、D.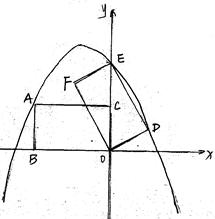
查看答案和解析>>
科目:初中数学 来源: 题型:
 中,
中, ,
, ,以
,以 为直径的
为直径的 与
与 相切于
相切于 .已知
.已知 ,边
,边 比
比 大6.
大6.
 、
、 的长.
的长. 上是否存在一动点
上是否存在一动点 ,使以
,使以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出
相似?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2011年浙江省杭州市萧山区中考数学模拟试卷 题型:解答题
(11·贵港)(本题满分11分)
如图所示,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
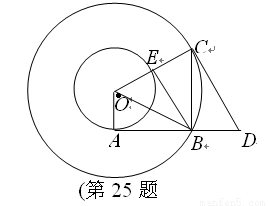
(1)求证:△AOB∽△BDC;
(2)设大圆的半径为x,CD的长为y:
① 求y与x之间的函数关系式;
② 当BE与小圆相切时,求x的值.
查看答案和解析>>
科目:初中数学 来源:2010年安徽省芜湖市毕业学业考试模拟试卷数学卷 题型:解答题
(本小题满分12分)如图所示,在梯形 中,
中, ,
,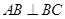 ,以
,以 为直径的
为直径的 与
与 相切于
相切于 .已知
.已知 ,边
,边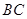 比
比 大6.
大6.

(1)求边 、
、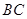 的长.
的长.
(2)在直径 上是否存在一动点
上是否存在一动点 ,使以
,使以 、
、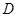 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出
相似?若存在,求出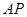 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com