
”¾ĢāÄæ”æĄū“ļ¾ĻśµźĪŖij¹¤³§“śĻśŅ»ÖÖ½ØÖž²ÄĮĻ£ØÕāĄļµÄ“śĻśŹĒÖø³§¼ŅĻČĆā·ŃĢį¹©»õŌ“£¬“ż»õĪļŹŪ³öŗóŌŁ½ųŠŠ½įĖć£¬Ī“ŹŪ³öµÄÓɳ§¼ŅøŗŌš“¦Ąķ£©£®µ±Ćæ¶ÖŹŪ¼ŪĪŖ260ŌŖŹ±£¬ŌĀĻśŹŪĮæĪŖ45¶Ö£®øĆ¾ĻśµźĪŖĢįøß¾ÓŖĄūČó£¬×¼±ø²ÉČ”½µ¼ŪµÄ·½Ź½½ųŠŠ“ŁĻś£®¾ŹŠ³”µ÷²é·¢ĻÖ£ŗµ±Ćæ¶ÖŹŪ¼ŪĆæĻĀ½µ10ŌŖŹ±£¬ŌĀĻśŹŪĮæ¾Ķ»įŌö¼Ó7.5¶Ö£®×ŪŗĻæ¼ĀĒø÷ÖÖŅņĖŲ£¬ĆæŹŪ³öŅ»¶Ö½ØÖž²ÄĮĻ¹²ŠčÖ§ø¶³§¼Ņ¼°ĘäĖü·ŃÓĆ100ŌŖ£®
£Ø1£©µ±Ćæ¶ÖŹŪ¼ŪŹĒ240ŌŖŹ±£¬¼ĘĖć“ĖŹ±µÄŌĀĻśŹŪĮ棻
£Ø2£©ŌŚ×ńŃ”°±”Ąū¶ąĻś”±µÄŌŌņĻĀ£¬ĪŹĆæ¶Ö²ÄĮĻŹŪ¼ŪĪŖ¶ąÉŁŹ±£¬øĆ¾ĻśµźµÄŌĀĄūČóĪŖ9000ŌŖ£æ
£Ø3£©Š”¾²Ėµ£ŗ”°µ±ŌĀĄūČó×ī“óŹ±£¬ŌĀĻśŹŪ¶īŅ²×ī“ó£®”±ÄćČĻĪŖ¶ŌĀš£æĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©60£»£Ø2£©200ŌŖ£»£Ø3£©Š”¾²ĖµµÄ²»¶Ō£®
”¾½āĪö”æ
£Ø1£©ŅņĪŖĆæ¶ÖŹŪ¼ŪĆæĻĀ½µ10ŌŖŹ±£¬ŌĀĻśŹŪĮæ¾Ķ»įŌö¼Ó7.5¶Ö£¬¾Ż“ĖæÉĒó³öĆæ¶ÖŹŪ¼ŪŹĒ240ŌŖŹ±£¬“ĖŹ±µÄŌĀĻśŹŪĮ棻
£Ø2£©Éčµ±ŹŪ¼ŪĪŖĆæ¶ÖxŌŖŹ±£¬øĆ¾ĻśµźµÄŌĀĄūČóĪŖ9000ŌŖ£¬øł¾Żµ±Ćæ¶ÖŹŪ¼ŪĪŖ260ŌŖŹ±£¬ŌĀĻśŹŪĮæĪŖ45¶Ö£¬ĆæŹŪ³öŅ»¶Ö½ØÖž²ÄĮĻ¹²ŠčÖ§ø¶³§¼Ņ¼°ĘäĖü·ŃÓĆ100ŌŖ£¬Ćæ¶ÖŹŪ¼ŪĆæĻĀ½µ10ŌŖŹ±£¬ŌĀĻśŹŪĮæ¾Ķ»įŌö¼Ó7.5¶Ö£¬ĒŅµ±ŌĀĄūČóĪŖ9000ŌŖ£¬ŅŌ9000ŌŖ×÷ĪŖµČĮæ¹ŲĻµµÄŅ»·½ĮŠ³ö·½³ĢĒó½ā¼“æÉ£»
£Ø3£©¼ŁÉčµ±ŌĀĄūČó×ī“óŹ±£¬xĪŖ210ŌŖ£¬¶ųøł¾ŻĢāŅāµĆxĪŖ160ŌŖŹ±£¬ŌĀĻśŹŪ¶ī×ī“󣬓ӶųµĆ³ö“š°ø.
½ā£ŗ£Ø1£©µ±Ćæ¶ÖŹŪ¼ŪŹĒ240ŌŖŹ±£¬
“ĖŹ±µÄŌĀĻśŹŪĮæĪŖ£ŗ45+![]() ”Į7.5£½60£Ø¶Ö£©£»
”Į7.5£½60£Ø¶Ö£©£»
“š£ŗµ±Ćæ¶ÖŹŪ¼ŪŹĒ240ŌŖŹ±£¬“ĖŹ±µÄŌĀĻśŹŪĮæĪŖ60¶Ö.
£Ø2£©Éčµ±ŹŪ¼Ū¶ØĪŖĆæ¶ÖxŌŖŹ±£¬
ÓÉĢāŅā£¬æÉĮŠ·½³Ģ£Øx©100£©£Ø45+![]() ”Į7.5£©£½9000£®
”Į7.5£©£½9000£®
»Æ¼ņµĆx2©420x+44000£½0£®
½āµĆx1£½200£¬x2£½220£®
“š£ŗ×ńŃ”°±”Ąū¶ąĻś”±µÄŌŌņĻĀ£¬Ćæ¶Ö²ÄĮĻŹŪ¼ŪĪŖ200ŌŖŹ±£¬øĆ¾ĻśµźµÄŌĀĄūČóĪŖ9000ŌŖ.
£Ø3£©ĪŅČĻĪŖ£¬Š”¾²ĖµµÄ²»¶Ō£®
”ßÓÉ£Ø2£©ÖŖ£¬x2©420x+44000£½0£¬
”ąµ±ŌĀĄūČó×ī“óŹ±£¬xĪŖ210ŌŖ£®
ĄķÓÉ£ŗµ±ŌĀĄūČó×ī“óŹ±£¬xĪŖ210ŌŖ£¬
¶ų¶ŌÓŚŌĀĻśŹŪ¶ī![]() Ą“Ėµ£¬
Ą“Ėµ£¬
µ±xĪŖ160ŌŖŹ±£¬ŌĀĻśŹŪ¶īW×ī“ó£®
”ąµ±xĪŖ210ŌŖŹ±£¬ŌĀĻśŹŪ¶īW²»ŹĒ×ī“ó£®
”ąŠ”¾²ĖµµÄ²»¶Ō£®


 ѧ¶ųÓÅŹīĘŚĻĪ½ÓÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø
ѧ¶ųÓÅŹīĘŚĻĪ½ÓÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø Happy holiday»¶ĄÖ¼ŁĘŚŹī¼Ł×÷Ņµ¹ć¶«ČĖĆń³ö°ęÉēĻµĮŠ“š°ø
Happy holiday»¶ĄÖ¼ŁĘŚŹī¼Ł×÷Ņµ¹ć¶«ČĖĆń³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
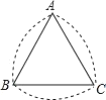
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾µÄĒś±ßČż½ĒŠĪæÉ°“ĻĀŹö·½·Ø×÷³ö£ŗ×÷µČ±ßČż½ĒŠĪ![]() £»·Ö±šŅŌµć
£»·Ö±šŅŌµć![]() £¬
£¬![]() £¬
£¬![]() ĪŖŌ²ŠÄ£¬ŅŌ
ĪŖŌ²ŠÄ£¬ŅŌ![]() µÄ³¤ĪŖ°ė¾¶×÷
µÄ³¤ĪŖ°ė¾¶×÷![]() £¬
£¬![]() £¬
£¬![]() £®Čż¶Ī»”ĖłĪ§³ÉµÄĶ¼ŠĪ¾ĶŹĒŅ»øöĒś±ßČż½ĒŠĪ£¬Čē¹ūŅ»øöĒś±ßČż½ĒŠĪµÄÖܳ¤ĪŖ
£®Čż¶Ī»”ĖłĪ§³ÉµÄĶ¼ŠĪ¾ĶŹĒŅ»øöĒś±ßČż½ĒŠĪ£¬Čē¹ūŅ»øöĒś±ßČż½ĒŠĪµÄÖܳ¤ĪŖ![]() £¬ÄĒĆ“ÕāøöĒś±ßČż½ĒŠĪµÄĆ껿ŹĒ___________£®
£¬ÄĒĆ“ÕāøöĒś±ßČż½ĒŠĪµÄĆ껿ŹĒ___________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĮāŠĪABCD±ß³¤ĪŖ4£¬”ĻA£½60”ć£¬MŹĒAD±ßµÄÖŠµć£¬NŹĒAB±ßÉĻŅ»¶Æµć£¬½«”÷AMNŃŲMNĖłŌŚµÄÖ±Ļß·ÕŪµĆµ½”÷A”äMN£¬Į¬½ÓA”äC£¬ŌņA”äCµÄ×īŠ”ÖµŹĒ£Ø £©

A.2![]() B.
B.![]() +1C.2
+1C.2![]() ©2D.3
©2D.3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔ÕÅÓĆ4ÕÅĻąĶ¬µÄŠ”Ö½Ģõ×ö³É¼×”¢ŅŅ”¢±ū”¢¶”4Ö§Ē©£¬·ÅŌŚŅ»øöŗŠ×ÓÖŠ£¬½ĮŌČŗóĻČ“ÓŗŠ×ÓÖŠČĪŅā³é³ö1Ö§Ē©(²»·Å»Ų)£¬ŌŁ“ÓŹ£ÓąµÄ3Ö§Ē©ÖŠČĪŅā³é³ö1Ö§Ē©£®
(1)Š”ÕŵŚŅ»“Ī³éµ½µÄŹĒŅŅĒ©µÄøÅĀŹŹĒ £»
(2)Ēó³é³öµÄĮ½Ö§Ē©ÖŠ£¬1Ö§ĪŖ¼×Ē©”¢1Ö§ĪŖ±ūĒ©µÄøÅĀŹ(ÓĆ»Ź÷דĶ¼»ņĮŠ±ķ·ØĒó½ā)£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
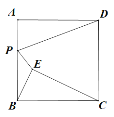
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÕż·½ŠĪABCDµÄ±ß³¤ĪŖ8£¬µćEŹĒÕż·½ŠĪÄŚ²æŅ»µć£¬Į¬½ÓBE£¬CE£¬ĒŅ”ĻABE£½”ĻBCE£¬µćPŹĒAB±ßÉĻŅ»¶Æµć£¬Į¬½Ó PD£¬PE£¬ŌņPD+PE³¤¶ČµÄ×īŠ”ÖµĪŖ£Ø £©
A.![]() B.
B.![]()
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
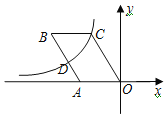
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬OABCµÄ¶„µćB”¢CŌŚµŚ¶žĻóĻŽ£¬µćDĪŖAB±ßµÄÖŠµć£¬·“±ČĄżŗÆŹży£½![]() ŌŚµŚ¶žĻóĻŽµÄĶ¼Ļó¾¹żC”¢DĮ½µć£®ČōµćAµÄ×ų±źŹĒ£Ø©2
ŌŚµŚ¶žĻóĻŽµÄĶ¼Ļó¾¹żC”¢DĮ½µć£®ČōµćAµÄ×ų±źŹĒ£Ø©2![]() £¬0£©£¬tan”ĻCOA£½3£¬ŌņkµÄÖµĪŖ_____£®
£¬0£©£¬tan”ĻCOA£½3£¬ŌņkµÄÖµĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy£½![]() x2£«bx£«c¹żµćA(3, 0)”¢µćB(0, 3)£®µćM(m, 0)ŌŚĻ߶ĪOAÉĻ£ØÓėµćA”¢O²»ÖŲŗĻ£©£¬¹żµćM×÷xÖįµÄ“¹ĻßÓėĻ߶ĪAB½»ÓŚµćP£¬ÓėÅ×ĪļĻß½»ÓŚµćQ£¬ĮŖ½įBQ£®
x2£«bx£«c¹żµćA(3, 0)”¢µćB(0, 3)£®µćM(m, 0)ŌŚĻ߶ĪOAÉĻ£ØÓėµćA”¢O²»ÖŲŗĻ£©£¬¹żµćM×÷xÖįµÄ“¹ĻßÓėĻ߶ĪAB½»ÓŚµćP£¬ÓėÅ×ĪļĻß½»ÓŚµćQ£¬ĮŖ½įBQ£®
£Ø1£©ĒóÅ×ĪļĻß±ķ“ļŹ½£»
£Ø2£©ĮŖ½įOP£¬µ±”ĻBOP£½”ĻPBQŹ±£¬ĒóPQµÄ³¤¶Č£»
£Ø3£©µ±”÷PBQĪŖµČŃüČż½ĒŠĪŹ±£¬ĒómµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½Ś¼ŁČÕĘŚ¼äĻņ”¢Ä³ÉĢ³”×éÖÆÓĪĻ·£¬Ö÷³ÖČĖĒėČżĪ»¼Ņ³¤·Ö±š“ų×Ō¼ŗµÄŗ¢ÓŚ²Ī¼ÓÓĪĻ·£¬A”¢B”¢C·Ö±š±ķŹ¾Ņ»Ī»¼Ņ³¤£¬ĖūĆĒµÄŗ¢×Ó·Ö±š¶ŌÓ¦µÄŹĒa£¬b£¬![]() ČōÖ÷³ÖČĖ·Ö±š“ÓČżĪ»¼Ņ³¤ŗĶČżĪ»ŗ¢ÓčÖŠø÷Ń”Ņ»ČĖ²Ī¼ÓÓĪĻ·£®
ČōÖ÷³ÖČĖ·Ö±š“ÓČżĪ»¼Ņ³¤ŗĶČżĪ»ŗ¢ÓčÖŠø÷Ń”Ņ»ČĖ²Ī¼ÓÓĪĻ·£®
![]() ČōŅŃє֊¼Ņ³¤A£¬ŌņĒ”ŗĆє֊×Ō¼ŗŗ¢×ÓµÄøÅĀŹŹĒ______£®
ČōŅŃє֊¼Ņ³¤A£¬ŌņĒ”ŗĆє֊×Ō¼ŗŗ¢×ÓµÄøÅĀŹŹĒ______£®
![]() ĒėÓĆ»Ź÷דĶ¼»ņĮŠ±ķ·ØĒó³ö±»Ń”ÖŠµÄĒ”ŗĆŹĒĶ¬Ņ»¼ŅĶ„³ÉŌ±µÄøÅĀŹ£®
ĒėÓĆ»Ź÷דĶ¼»ņĮŠ±ķ·ØĒó³ö±»Ń”ÖŠµÄĒ”ŗĆŹĒĶ¬Ņ»¼ŅĶ„³ÉŌ±µÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”°3.15”±Ö²Ź÷½Ś»ī¶Æŗ󣬶ŌŌŌĻĀµÄ¼×”¢ŅŅ”¢±ū”¢¶”ĖÄøöĘ·Öֵď÷Ćē½ųŠŠ³É»īĀŹ¹Ū²ā£¬ŅŌĻĀŹĒøł¾Ż¹Ū²āŹż¾ŻÖĘ³ÉµÄĶ³¼ĘĶ¼±ķµÄŅ»²æ·Ö£ŗ
ŌŌĻĀµÄø÷Ę·ÖÖŹ÷ĆēæĆŹżĶ³¼Ę±ķ | ||||
Ö²Ź÷Ę·ÖÖ | ¼×ÖÖ | ŅŅÖÖ | ±ūÖÖ | ¶”ÖÖ |
Ö²Ź÷æĆŹż | 150 | 125 | 125 | |

Čō¾¹Ū²ā¼ĘĖćµĆ³ö±ūÖÖŹ÷ĆēµÄ³É»īĀŹĪŖ89.6%£¬ĒėÄćøł¾ŻŅŌÉĻŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Õā“ĪŌŌĻĀµÄĖÄøöĘ·Öֵď÷Ćē¹² æĆ£¬ŅŅĘ·ÖÖŹ÷Ćē æĆ£»
£Ø2£©Ķ¼1ÖŠ£¬¼× %”¢ŅŅ %£¬²¢½«Ķ¼2²¹³äĶźÕū£»
£Ø3£©ĒóÕā“ĪÖ²Ź÷»ī¶ÆµÄŹ÷Ćē³É»īĀŹ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com