
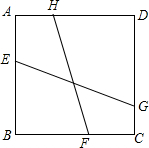
 如图,正方形ABCD中,点E、F、G、H分别是在边AB、BC、CD、DA上,且EG与FH的夹角为45°,若正方形ABCD的边长是1.FH=$\frac{\sqrt{5}}{2}$,则EG的长度是$\frac{\sqrt{10}}{3}$.
如图,正方形ABCD中,点E、F、G、H分别是在边AB、BC、CD、DA上,且EG与FH的夹角为45°,若正方形ABCD的边长是1.FH=$\frac{\sqrt{5}}{2}$,则EG的长度是$\frac{\sqrt{10}}{3}$. 分析 可过点A作AM∥HF交BC于点M,过点A作AN∥EG交CD于点N,将△AND绕点A旋转到△APB,不难得出△APM和△ANM全等,那么可得出PM=MN,而MB的长可在RT△ABM中根据AB和AM(即HF的长)求出.如果设DN=x,那么NM=PM=BM+x,MC=BC-BM=1-BM,因此可在直角三角形MNC中用勾股定理求出DN的长,进而可在RT△AND中求出AN即EG的长.
解答 解:过点A作AM∥HF交BC于点M,过点A作AN∥EG交CD于点N,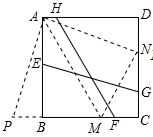
∵AB=1,AM=FH=$\frac{\sqrt{5}}{2}$,
在Rt△ABM中,BM=$\sqrt{A{M}^{2}-A{B}^{2}}$=$\frac{1}{2}$,将△AND绕点A旋转到△APB,
∵EG与FH的夹角为45°,
∴∠MAN=45°,
∴∠DAN+∠MAB=45
即∠PAM=∠MAN=45°,
从而△APM≌△ANM,
∴PM=NM,
设DN=x,则NC=1-x,NM=PM=$\frac{1}{2}$+x
在Rt△CMN中,($\frac{1}{2}$+x)2=$\frac{1}{4}$+(1-x)2,
解得x=$\frac{1}{3}$,
∴EG=AN=$\sqrt{1+{x}^{2}}$=$\frac{\sqrt{10}}{3}$,
答:EG的长为$\frac{\sqrt{10}}{3}$.
故答案为$\frac{\sqrt{10}}{3}$.
点评 本题主要考查了正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质、图形的旋转变换等知识.通过辅助线或图形的旋转将所求的线段与已知的线段构建到一对全等或相似的三角形中是本题的基本思路.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
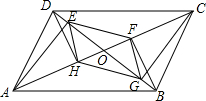 如图所示,平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,BF⊥AC于点F,CG⊥BD于点G,DH⊥AC于点H,求证:四边形EFGH是平行四边形.
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,BF⊥AC于点F,CG⊥BD于点G,DH⊥AC于点H,求证:四边形EFGH是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
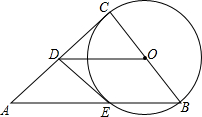 在△ABC中,∠ACB=90°,以BC为直径作圆O,交斜边AB于E,D是AC的中点,连接DE.
在△ABC中,∠ACB=90°,以BC为直径作圆O,交斜边AB于E,D是AC的中点,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
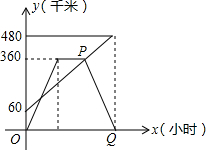 甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图:
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
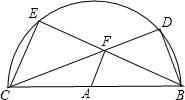 BC是半圆⊙A的直径,点D,E是圆上两点,并且∠DAE是直角,点F是弦CD、BE的交点.
BC是半圆⊙A的直径,点D,E是圆上两点,并且∠DAE是直角,点F是弦CD、BE的交点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 110°,70° | B. | 105°,75° | C. | 100°,70° | D. | 110°,80° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com