
【题目】已知:如图,AB=AC,AE=AF,连结BF,CE,交于O,连结AO.求证:

(1)∠B=∠C
(2)AO平分∠BAC
【答案】(1)答案见解析;(2)答案见解析
【解析】
(1)由SAS证得△AEC≌△AFB,即可得出结论;
(2)先证△EBO≌△FCO,得出OB=OC,再由SSS证明△AOB≌△AOC,即可得出结论.
(1)在△AEC与△AFB中,∵AE=AF,∠EAF=∠EAF,AC=AB,∴△AEC≌△AFB(SAS),∴∠C=∠B;
(2)∵AB=AC,AE=AF,∴BE=CF.
在△BEO和△CFO中,∵∠B=∠C,∠EOB=∠FOC,BE=CF,∴△BEO≌△CFO,∴BO=CO.
在△AOB和△AOC中,∵AB=AC,AO=AO,OB=OC,∴△AOB≌△AOC,∴∠BAO=∠CAO,∴AO平分∠BAC.


科目:初中数学 来源: 题型:
【题目】 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
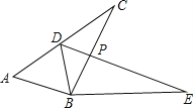
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;
(2)求△DCP与△BPE的周长和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点![]() 点M不与B,C重合
点M不与B,C重合![]() ,
,![]() ,CN与AB交于点N,连接OM,ON,
,CN与AB交于点N,连接OM,ON,![]() 下列五个结论:
下列五个结论:![]() ≌
≌![]() ;
;![]() ≌
≌![]() ;
;![]() ∽
∽![]() ;
;![]() ;
;![]() 若
若![]() ,则
,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是
,其中正确结论的个数是![]()
![]()

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在△ABC中,∠BAC=90,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.E证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D. A.E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请问结论DE=BD+CE是否成立,若成立,请你给证明:若不存在,请说明理由。
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,D. A.E三点都在直线m上,且∠BDA=∠AEC=∠BAC,只出现m与BC的延长线交于点F,若BD=5,DE=7,EF=2CE,求△ABD与△ABF的面积之比。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,则∠AMN+∠ANM的角度为________.
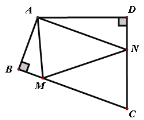
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应的点之间的距离;
对应的点之间的距离;
例 1.解方程![]() ,因为在数轴上到原点的距离为
,因为在数轴上到原点的距离为![]() 的点对应的数为
的点对应的数为![]() ,所以方程
,所以方程![]() 的解为
的解为![]() .
.
例 2.解不等式![]() ,在数轴上找出
,在数轴上找出![]() 的解(如图),因为在数轴上到
的解(如图),因为在数轴上到![]() 对应的点的距离等于
对应的点的距离等于![]() 的点对应的数为
的点对应的数为![]() 或
或![]() ,所以方程
,所以方程![]() 的解为
的解为![]() 或
或![]() ,因此不等式
,因此不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
参考阅读材料,解答下列问题:
(1)方程![]() 的解为 ;
的解为 ;
(2)解不等式:![]() ;
;
(3)解不等式:.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“3.15”植树节活动后,对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分:
栽下的各品种树苗棵数统计表 | ||||
植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
植树棵数 | 150 | 125 | 125 | |

若经观测计算得出丙种树苗的成活率为89.6%,请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共 棵,乙品种树苗 棵;
(2)图1中,甲 %、乙 %,并将图2补充完整;
(3)求这次植树活动的树苗成活率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com