
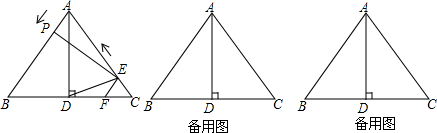
分析 (1)先证得DE=EC,然后根据平行四边形的性质得出PB=EF,即可证得PB=EC,从而求得t=5-t,解方程即可求得;
(2)根据勾股定理求得AD=4,过E点作EH⊥BC于H,根据平行线的性质得出$\frac{EH}{4}$=$\frac{t}{5}$=$\frac{FC}{6}$,求得EH=$\frac{4}{5}$t,FC=$\frac{6}{5}$t,然后分①当0<t≤$\frac{5}{2}$时,DF=3-$\frac{6}{5}$t,②当$\frac{5}{2}$<t<5时,DF=$\frac{6}{5}$t-3,根据三角形面积公式列出方程,解方程即可求得;
(3)作CM⊥AB于M,EN⊥AB于N,根据三角形相似对应边成比例求得CM=$\frac{24}{5}$,BM=$\frac{18}{5}$,AM=$\frac{7}{5}$,进而求得EN=$\frac{24}{5}$-$\frac{24}{25}$t,AN=$\frac{7}{5}$-$\frac{7}{25}$t,PN=t-($\frac{7}{5}$-$\frac{7}{25}$t)=$\frac{32}{25}$t-$\frac{7}{5}$,根据勾股定理得出PE2=($\frac{24}{5}$-$\frac{24}{25}$t)2+($\frac{32}{25}$t-$\frac{7}{5}$)2=$\frac{64}{25}$t2-$\frac{64}{5}$t+25,然后分三种情况分别讨论即可求得.
解答  解:(1)∵四边形PBFE是平行四边形,
解:(1)∵四边形PBFE是平行四边形,
∴PB=EF,
∵AB=AC,
∴∠B=∠C,
∵EF∥AB,
∴∠EFC=∠B,
∴∠EFC=∠C,
∴EF=EC,
∵AP=EC=t,
∴EF=t,PB=5-t,
∴t=5-t,
解得t=$\frac{5}{2}$;
(2)∵AB=AC,AD⊥BC,
∴BD=CD=3,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
过E点作EH⊥BC于H,
∵AD⊥BC,
∴EH∥AD,
∴$\frac{EH}{AD}$=$\frac{EC}{AC}$=$\frac{CF}{BC}$,
即$\frac{EH}{4}$=$\frac{t}{5}$=$\frac{FC}{6}$,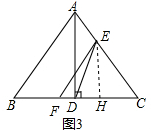
∴EH=$\frac{4}{5}$t,FC=$\frac{6}{5}$t,
①当0<t≤$\frac{5}{2}$时,DF=3-$\frac{6}{5}$t,
∴△DEF的面积=$\frac{1}{2}$DF•EH=$\frac{1}{2}$×$\frac{4}{5}$t×(3-$\frac{6}{5}$t)=$\frac{3}{4}$,
解得t=$\frac{5}{4}$;
②当$\frac{5}{2}$<t<5时,DF=$\frac{6}{5}$t-3,
∴△DEF的面积=$\frac{1}{2}$DF•EH=$\frac{1}{2}$×($\frac{6}{5}$t-3)×$\frac{4}{5}$t=$\frac{3}{4}$,
解得,t1=$\frac{5+5\sqrt{2}}{4}$,t2=$\frac{5-5\sqrt{2}}{4}$(舍去);
综上所述,t=$\frac{5}{4}$或$\frac{5+5\sqrt{2}}{4}$时,△DEF的面积为$\frac{3}{4}$cm2;
(3)如图4,作CM⊥AB于M,EN⊥AB于N,
∵∠CMB=∠ADB=90°,∠ABD=∠MBC,
∴△MBC∽△DBA,
∴$\frac{CM}{AD}$=$\frac{BC}{AB}$=$\frac{BM}{BD}$,即$\frac{CM}{4}$=$\frac{6}{5}$=$\frac{BM}{3}$
∴CM=$\frac{24}{5}$,BM=$\frac{18}{5}$,
∴AM=$\frac{7}{5}$,
∵CM⊥AB,EN⊥AB,
∴EN∥CM,
∴$\frac{EN}{CM}$=$\frac{AE}{AC}$=$\frac{AN}{AM}$,即$\frac{EN}{\frac{24}{5}}$=$\frac{5-t}{5}$=$\frac{AN}{\frac{7}{5}}$
∴EN=$\frac{24}{5}$-$\frac{24}{25}$t,AN=$\frac{7}{5}$-$\frac{7}{25}$t,
∴PN=t-($\frac{7}{5}$-$\frac{7}{25}$t)=$\frac{32}{25}$t-$\frac{7}{5}$,
∴PE2=($\frac{24}{5}$-$\frac{24}{25}$t)2+($\frac{32}{25}$t-$\frac{7}{5}$)2=$\frac{64}{25}$t2-$\frac{64}{5}$t+25,
∵EF=t,PF=PB=5-t,
①EF=PF时,t=$\frac{5}{2}$;
②PE2=PF2时,$\frac{64}{25}$t2-$\frac{64}{5}$t+25=25-10t+t2
解得t1=0(舍),t2=$\frac{70}{39}$;
③EF2=PE2时,$\frac{64}{25}$t2-$\frac{64}{5}$t+25=t2
解得t1=5(舍),t2=$\frac{125}{39}$,
综上所述,t=$\frac{5}{2}$或$\frac{70}{39}$或$\frac{125}{39}$时,△PEF是等腰三角形.
点评 本题是四边形的综合题,考查了平行四边形的判定和性质,等腰三角形的判定和性质,三角形相似的判定和性质,勾股定理的应用以及三角形面积等,作出辅助线构建直角三角形是解题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
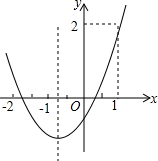 二次函数y=ax2+bx+c的图象如图所示,则下列说法:①abc<0;②2a>b;③a+c>1;④9a+c<3b+2,其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,则下列说法:①abc<0;②2a>b;③a+c>1;④9a+c<3b+2,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
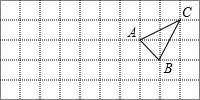 如图,在边长为1的正方形网格中,有一格点△ABC,已知A、B、C三点的坐标分别是A(1,0)、B(2,-1)、C(3,1).
如图,在边长为1的正方形网格中,有一格点△ABC,已知A、B、C三点的坐标分别是A(1,0)、B(2,-1)、C(3,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com