
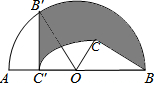
 如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.
如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2. 分析 根据直角三角形的性质求出OC、BC,根据扇形面积公式计算即可.
解答 解:∵∠BOC=60°,∠BCO=90°,
∴∠OBC=30°,
∴OC=$\frac{1}{2}$OB=1,BC=$\sqrt{3}$,
则边BC扫过区域的面积为:$\frac{120π×{2}^{2}}{360}$+$\frac{1}{2}$×$\sqrt{3}$×1-$\frac{120π×{1}^{2}}{360}$-$\frac{1}{2}$×$\sqrt{3}$×1=πcm2.
故答案为:π.
点评 本题考查的是扇形面积的计算、旋转变换的性质,掌握扇形的面积公式:S=$\frac{nπ{R}^{2}}{360}$是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有400人.
如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有400人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
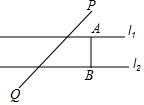 如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4$\sqrt{30}$,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=16.
如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4$\sqrt{30}$,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
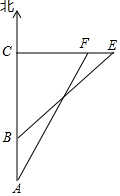 钓鱼岛自古以来就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视检测.如图,E、F为钓鱼岛东西两端.某日,中国一艘海监船从A点向正北方向巡航,其航线距离钓鱼岛最近距离CF=20$\sqrt{3}$海里,在A点测得钓鱼岛最西端F在点A的北偏东30°方向,航线20海里后到达B点,测得最东端E点在B的东北方向(C、F、E在同一直线上).($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{7}$≈2.65,结果精确到0.1)
钓鱼岛自古以来就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视检测.如图,E、F为钓鱼岛东西两端.某日,中国一艘海监船从A点向正北方向巡航,其航线距离钓鱼岛最近距离CF=20$\sqrt{3}$海里,在A点测得钓鱼岛最西端F在点A的北偏东30°方向,航线20海里后到达B点,测得最东端E点在B的东北方向(C、F、E在同一直线上).($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{7}$≈2.65,结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
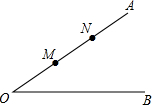 如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是x=0或x=4$\sqrt{2}$-4或4<x<4$\sqrt{2}$.
如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是x=0或x=4$\sqrt{2}$-4或4<x<4$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com