
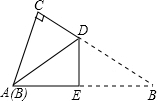
 (2004•泰安)有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图),则CD等于( )
(2004•泰安)有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图),则CD等于( )科目:初中数学 来源: 题型:
| 身高 | 148 | 151 | 154 | 155 | 157 | 158 | 160 | 161 | 162 | 164 |
| 人数 | 1 | 1 | 2 | 1 | 2 | 3 | 4 | 3 | 4 | 5 |
| 身高 | 165 | 166 | 167 | 168 | 170 | 171 | 173 | 175 | 177 | 179 |
| 人数 | 2 | 3 | 6 | 1 | 4 | 2 | 3 | 1 | 1 | 1 |
| 分 组 | 频 数 | 频 率 |
| 147.5~151.5 | 2 | 0.04 |
| 151.5~155.5 | 3 | 0.06 |
| 155.5~159.5 | 5 | 0.10 |
| 159.5~163.5 | 11 | 0.22 |
| 163.5~167.5 | 16 16 |
0.32 0.32 |
| 167.5~171.5 | 7 7 |
0.14 0.14 |
| 171.5~175.5 | 4 | 0.08 |
| 175.5~179.5 | 2 | 0.04 |
| 合 计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2004•泰安)如图,在△ABC中,AB=3,BC=2
(2004•泰安)如图,在△ABC中,AB=3,BC=2| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
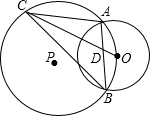 (2004•泰安)已知:如图,⊙P与⊙O相交于点A、B,且⊙P经过点O,点C是⊙P的优弧AB上任意一点(不与点A、B重合),弦OC交公共弦AB于点D,连接CA、CB.
(2004•泰安)已知:如图,⊙P与⊙O相交于点A、B,且⊙P经过点O,点C是⊙P的优弧AB上任意一点(不与点A、B重合),弦OC交公共弦AB于点D,连接CA、CB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com