

分析 如图,DE=0.8,EF=0.6,则DF=1,作DQ⊥DF交EF于Q,即使太阳光线垂直于DQ,利用等角的余角相等得到∠Q=∠EDF,在Rt△EDF中,利用三角函数的定义得到cos∠EDF=0.8,sin∠EDF=0.6,再根据相似的判定易得△MNH∽△DQE,则∠MNH=∠Q,在Rt△MNH中,根据三角函数的定义可计算出NH=1.44,MH=1.08;则在Rt△ANH中,利用正切的定义计算出AH=0.576,然后利用MA=MH-AH进行计算即可.
解答 解: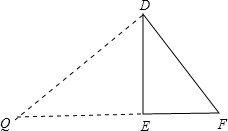 如图,DE=0.8,EF=0.6,则DF=1,
如图,DE=0.8,EF=0.6,则DF=1,
作DQ⊥DF交EF于Q,
∴∠Q=∠EDF,
在Rt△EDF中,cos∠EDF=$\frac{DE}{DF}$=$\frac{0.8}{1}$=0.8,sin∠EDF=$\frac{0.6}{1}$=0.6,
∵△MNH∽△DQE,
∴∠MNH=∠Q,
在Rt△MNH中,∵cos∠MNH=$\frac{NH}{MN}$=0.8,sin∠MNH=$\frac{MH}{MN}$=0.6,
∴NH=0.8×1.8=1.44,MH=0.6×1.8=1.08,
在Rt△ANH中,∵tan∠ANH=tan21.8°=$\frac{AH}{NH}$,
∴AH=1.44×0.4=0.576,
∴MA=MH-AH=1.08-0.576=0.504(m).
答:符合安装要求的支架MA的长度为0.504米.
点评 本题考查了解直角三角形的应用:将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题),根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
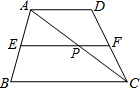 如图,梯形ABCD中,AD∥BC,EF是梯形的中位线,对角线AC交EF于P,若BC=10,EF=8,则PF=( )
如图,梯形ABCD中,AD∥BC,EF是梯形的中位线,对角线AC交EF于P,若BC=10,EF=8,则PF=( )| A. | 2 | B. | 5 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
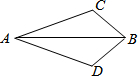 如图,已知∠CAB=∠DAB,则下列不能判定△ABC≌△ABD的条件是( )
如图,已知∠CAB=∠DAB,则下列不能判定△ABC≌△ABD的条件是( )| A. | ∠C=∠D | B. | AC=AD | C. | ∠CBA=∠DBA | D. | BC=BD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
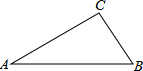 在△ABC中,∠ACB=90°,若∠A=30°,CA=6,则AB的长为,4$\sqrt{3}$,△ABC的面积为6$\sqrt{3}$.
在△ABC中,∠ACB=90°,若∠A=30°,CA=6,则AB的长为,4$\sqrt{3}$,△ABC的面积为6$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,一棵32米高的巨大杉树在海棠号台风中被刮断,树顶C落在离树根B点16米处,科研人员要看查看断痕A处的情况,在离树根B有5米的D处竖起一个梯子AD,请问这个梯子有多长?
如图所示,一棵32米高的巨大杉树在海棠号台风中被刮断,树顶C落在离树根B点16米处,科研人员要看查看断痕A处的情况,在离树根B有5米的D处竖起一个梯子AD,请问这个梯子有多长?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com