
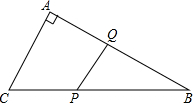
 ��ͼ����֪Rt��ABC�У���A=90�㣬AB=8��AC=6����Q��ÿ��1����λ���ٶȴ�B��A�˶���ͬʱ��P��ÿ��2����λ���ٶȴ�B��C��A�����˶������ǵ�A���ֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮
��ͼ����֪Rt��ABC�У���A=90�㣬AB=8��AC=6����Q��ÿ��1����λ���ٶȴ�B��A�˶���ͬʱ��P��ÿ��2����λ���ٶȴ�B��C��A�����˶������ǵ�A���ֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮���� ��1����P����Cʱ������ʱ��Ϊ5s������P��PD��AB�ڵ�D���������������ε����ʼ������d��t�Ĺ�ϵʽ��
��2���ֵ�P��BC���˶�����P��AC���˶���������������ۣ����ù��ɶ������PQ�ı���ʽ��
��3���ֵ�P��BC���˶�����P��AC���˶���������������ۣ��������������ε��������t��ֵ��
��� �⣺��1���ɹ��ɶ�����֪��BC=10��
��P��BC���˶�ʱ��0��t��5��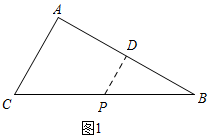 ����P��PD��AB�ڵ�D��
����P��PD��AB�ڵ�D��
��PD��AC��
���PBD�ס�CBA��
��$\frac{PD}{AC}=\frac{PB}{BC}$��
��PD=d��AC=6��PB=2t��BC=10��
��$\frac{d}{6}=\frac{2t}{10}$��
��d=$\frac{6}{5}$t��0��t��5����
��2��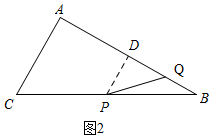 ��0��t��5����ͼ2��
��0��t��5����ͼ2��
�ɣ�1����֪��$\frac{BD}{AB}=\frac{PB}{BC}$��
��BD=$\frac{8}{5}$t��
��BQ=t��
��DQ=BD-BQ=$\frac{3}{5}t$��
���ɹ��ɶ�����֪��PQ=$\frac{3\sqrt{5}}{5}$t��
�൱t=5ʱ��PQ���ֵΪ3$\sqrt{5}$��
��5��t��8ʱ����ͼ3
��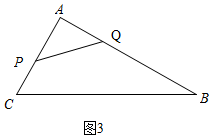 BQ=t��AQ=8-t��
BQ=t��AQ=8-t��
AP=6+10-2t=16-2t��
���ɹ��ɶ�����֪��PQ=${\sqrt{��16-2t��^{2}+��8-t��^{2}}}^{\;}$=$\sqrt{5{t}^{2}-80t+320}$=$\sqrt{5��t-8��^{2}}$
��t=5ʱ��PQ���ֵΪ3$\sqrt{5}$��
������������t=5ʱ����ʱPQ������ֵΪ3$\sqrt{5}$��
��3����0��t��5ʱ��
��$\frac{BQ}{BP}=\frac{AB}{BP}$��$\frac{BQ}{BP}=\frac{BP}{AB}$ʱ��
���PQB�ס�APB��
��$\frac{t}{2t}=\frac{8}{2t}$��$\frac{t}{2t}=\frac{2t}{8}$��
����t=8����ȥ����t=2��
��5��t��8ʱ��
��ʱ��APBʱֱ�������Σ���PQBʱ�۽������Σ�
��ʱ��PQB���APB�����ƣ�
����������t=2��
���� ���⿼�����������ε��ۺ��⣬�漰���ɶ��������κ��������ʣ����������ε����ʣ��������۵�˼�룬�ۺϳ̶Ƚϸߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
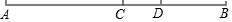 ��ͼ����֪��C���߶�AB���е㣬��D���߶�CB�ϣ���CD=$\frac{1}{3}$AC����AB=18cm����BD�ij���
��ͼ����֪��C���߶�AB���е㣬��D���߶�CB�ϣ���CD=$\frac{1}{3}$AC����AB=18cm����BD�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com