
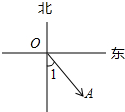
 如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )
如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )| A. | 商船在海岛的北偏西50°方向 | B. | 海岛在商船的北偏西40°方向 | ||
| C. | 海岛在商船的东偏南50°方向 | D. | 商船在海岛的东偏南40°方向 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-y)2=91 | B. | (x-y)2=81 | C. | x2+y2=511 | D. | x2+y2=63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com