
【题目】如图,放置的△OAB![]() ,△
,△![]() ,△
,△![]() ,…都是边长为2的等边三角形,边AO在
,…都是边长为2的等边三角形,边AO在![]() 轴上,点
轴上,点![]() 、
、![]() 、
、![]() …都在直线
…都在直线![]() 上,则点
上,则点![]() 的坐标为_______
的坐标为_______

【答案】(![]() ,2021)
,2021)
【解析】
延长A1B1交x轴于C,可证A1B1⊥x轴,由条件可求得∠B1OC=30°,利用直角三角形的性质可求得B1C=1,OC=![]() ,可求得B1的坐标,进而可求得A1的坐标,同理可求得A2、A3的坐标,则可得出规律,求得A2019的坐标.
,可求得B1的坐标,进而可求得A1的坐标,同理可求得A2、A3的坐标,则可得出规律,求得A2019的坐标.
解:如图,延长A1B1交x轴于C,
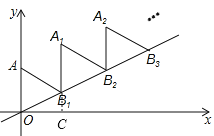
∵△OAB![]() ,△
,△![]() ,△
,△![]() ,…是等边三角形,且边长为2,
,…是等边三角形,且边长为2,
∴∠AOB1=60°,OB1=2,
∴∠B1OC=30°,![]() =60°,
=60°,
∴∠OB1C=60°,
∴∠OCB1=90°,
在Rt△B1OC中,可得B1C=1,OC=![]() ,
,
∴B1的坐标为(![]() ,1),
,1),
∴A1的坐标为(![]() ,3),
,3),
同理A2(2![]() ,4)、A3(3
,4)、A3(3![]() ,5),
,5),
∴An的坐标为(n![]() ,n+2),
,n+2),
∴A2019的坐标为(2019![]() ,2021),
,2021),
故答案为:(2019![]() ,2021).
,2021).


科目:初中数学 来源: 题型:
【题目】(1)操作发现如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决(设DF=x,AD=y.)
保持(1)中的条件不变,若DC=2DF,求![]() 的值;
的值;
(3)类比探求
保持(1)中条件不变,若DC=nDF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以直线x=![]() 对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y轴交于C(0,5),直线l与y轴交于点D.
对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y轴交于C(0,5),直线l与y轴交于点D.
(1)求抛物线的函数表达式;
(2)设直线l与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若![]() ,且△BCG与△BCD面积相等,求点G的坐标;
,且△BCG与△BCD面积相等,求点G的坐标;
(3)若在x轴上有且仅有一点P,使∠APB=90°,求k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,甲从家出发前往与家相距![]() 千米的旅游景点旅游,以
千米的旅游景点旅游,以![]() 千米/时的速度步行
千米/时的速度步行![]() 小时后,改骑自行车以
小时后,改骑自行车以![]() 千米/时的速度继续向目的地出发,乙在甲前面
千米/时的速度继续向目的地出发,乙在甲前面![]() 千米处,在甲出发
千米处,在甲出发![]() 小时后开车追赶甲,两人同时到达目的地.设甲、乙两人离甲家的距离
小时后开车追赶甲,两人同时到达目的地.设甲、乙两人离甲家的距离![]() (千米)与甲出发的时间
(千米)与甲出发的时间![]() (小时)之间的函数关系如图所示.
(小时)之间的函数关系如图所示.
(1)求乙的速度;
(2)求甲出发多长时间后两人第一次相遇;
(3)求甲出发几小时后两人相距![]() 千米. .
千米. .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点且
上一点且![]() ,过点
,过点![]() 画线段
画线段![]() ,使点
,使点![]() 在
在![]() 的边上且点
的边上且点![]() ,
,![]() 与
与![]() 的一个顶点组成的小三角形与
的一个顶点组成的小三角形与![]() 相似,则满足条件的线段
相似,则满足条件的线段![]() 的长度分别为________.
的长度分别为________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某所中学七、八、九年级各有6个班级,每个班级人数为50左右,根据实际情况,决定开设“A:乒乓球,B:篮球,C:跑步,D:跳绳”这四种项目.为了解学生喜欢哪一种项目,该学校体育组随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请结合图中信息解答下列问题:
(1)样本容量是________,请你为体育组提供一种较为合理的抽样方案;
(2)把条形统计图补充完整;
(3)该校贝贝、晶晶、洋洋和妮妮是学校的校园之星,现要从这四人中选出两人作为“阳光体育”运动形象代言人,贝贝和晶晶同时被抽到的概率是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com